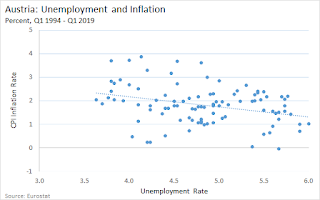
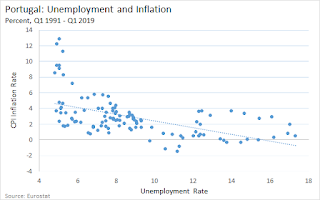
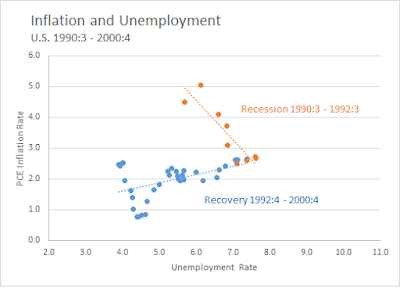
There are a lot of moving parts to the MMT program. I want to focus on one of these parts today: the relation between monetary and fiscal policy.
One thing I find appealing about MMT scholars is their attention to monetary history and
institutional details. I've learned a lot from them in this regard.
But as is often the case with details, one has to worry about whether they help
shed light on a specific question of interest, or whether they sometimes let us not see
the forest for the trees. And in terms of the broader picture, since I grew up
in that branch of macroeconomics that tries to take money, banking, and debt
seriously (i.e., not standard NK theory), I sometimes have a hard time understanding what all the fuss is
about. Much of standard monetary theory (SMT) seems perfectly consistent with
some of the ideas I seen discussed in MMT proponents; see, for example, The Failure to Inflate Japan.
This post is devoted to better
understanding a contribution by Eric Tymoigne. Eric is one of the people I go
to whenever I want to learn more about MMT (if you're interested in MMT, you
should follow him on Twitter @tymoignee). In this post, I discuss his
article "Modern Monetary Theory, and Interrelations Between the Treasury
and Central Bank: The Case of the United States." (JEI 2014). Passages quoted from his paper are highlighted in blue. The working
paper version of the paper can be found here. Eric has kindly agreed to respond to my comments and let me post our conversation. We had to some editing, hopefully this did not disrupt the flow too much. In any case, I hope you find it interesting. And, as always, feel free to join in on the conversation in the comments section below. -- DA
============================================================================
Perhaps what is meant is that MMT shows how existing self-imposed constraints on budgetary operations can be (or are) bypassed in reality. This leads us to question, however, concerning what those self-imposed constraints are doing there in the first place. Are they there by design and, if so, why? Or are they there by accident (and, if so, how in the world did this happen)?
DA: Eric, let's start with the opening paragraph:
One of the main contributions of modern money theory (MMT) has been
to explain why monetarily sovereign governments have a very flexible policy
space. Not only can they issue their own currency to spend and to service their
public debt denominated in their own unit of account, but also any self-imposed
constraint on budgetary operations can be easily bypassed.
I'm
curious to know what the contribution is here relative to standard monetary
theory (SMT). In SMT, the government can also issue its own currency to spend
and to service the public debt denominated in its own unit of account. So this
degree of "flexibility" is already accounted for. As for
"self-imposed constraints on budgetary operations," SMT takes several
approaches to this issue, depending on the purpose of the analysis. One
approach is to take these constraints as given and then to study their
implications. But it is also common to consolidate the central bank, treasury
and government into a single authority, which implies no self-imposed
constraints on budgetary operations.
Perhaps what is meant is that MMT shows how existing self-imposed constraints on budgetary operations can be (or are) bypassed in reality. This leads us to question, however, concerning what those self-imposed constraints are doing there in the first place. Are they there by design and, if so, why? Or are they there by accident (and, if so, how in the world did this happen)?
ET: Yes
consolidation is not unique to MMT as we have said repeatedly. Not only is it
used quite commonly in the economic literature, but also it is a common
rhetorical tool in economic talks, discourse, etc.
DA: Right, so everyone understands this (at least, they should)--it's perfectly consistent with standard monetary theory. So far, so good.
ET: Most
economists, politicians and the public don’t understand this or its
implications. They will interpret the above as saying that it is obvious that
the government can create money but it is not a normal way to proceed and it is
inflationary. MMT just pushes consolidation to its logical conclusions and
shows that institutional details do back those conclusions. In a consolidated
framework, the federal government can only implement spending by creating
money, this is not abnormal and it is not inflationary by itself. There is no
other way to find the necessary dollars to spend. Here is what consolidation means in terms of balance sheets:
For the federal government, taxes destroy currency
(L1 falls) and claims on non-fed sectors falls (A1 falls) (an alternative
offsetting operation is net worth of government rises). When US spends, it
credits accounts (L1 rises). Similarly, bond issuance does not lead to a gain
of any asset for the government; all it does is replace a non-interest earning government
liability (monetary base) with an interest-earning government liability (Treasury
securities).
DA: I am not going to argue against your accounting. As for bond-issuance, in
SMT, an open-market operation is modeled as a swap of zero-interest reserves
for interest-bearing treasuries. The interest on treasuries is explained by
their relative illiquidity (another self-imposed constraint). The economic
consequences of such a swap depends on a host of factors, which I'm sure you're
familiar with.
ET: Sure, in
addition, self-imposed financial constraints (e.g. debt ceiling, no direct
financing by the Fed, no monetary power for treasury) have been put in place at
various times with the argument that they impose discipline in public finances.
MMT argues, these financial constraints are not necessary and are bypassed
routinely through Treasury-Central Bank coordination.
DA: Sure, the standard view is that these
self-imposed constraints are designed to impose discipline in public finance.
The proposition that these financial constraints are or are not necessary, however, must be
based on a set of assumptions that may or may not be satisfied in reality. (The
fact that these constraints may be bypassed through Treasury-Central Bank
coordination does not seem relevant to me -- the conflict emphasized by SMT is
between an "independent" central bank and the legislative authority
(e.g., the Fed and Congress, not the Fed and Treasury). I'm not sure why a new
theory is needed here. We know, for example, that if the legislative branch of
government fully trusts itself (and future elected representatives) to behave
in a fiscally responsible manner, the notion of an "independent"
central bank (and other self-imposed constraints) makes little sense.
ET: Remember
that MMT emphasizes the irrelevance of financial/nominal constraints for
monetarily sovereign governments (bond vigilantes, risk of insolvency of social
security, etc.). One can do that by using the consolidated government (taxes
don’t finance, bonds don’t finance, government spends by crediting accounts,
etc.) or by using the unconsolidated government (the central bank helps the Treasury,
the Treasury helps the central bank). The second method conforms to actual
federal government operations but it is much less easy to use rhetorically and it
waters down the core point: government finances are never a financial issue as
long as monetary sovereignty applies.
Given that point, as you note, financial constraints are not only
irrelevant, but also disruptive and used for political games. MMT wants to make
government financial operations as smooth and flexible as possible. Once
society has decided how, and to what degree, government should be involved in
solving socioeconomic problems, finding the money should not be an issue when
monetary sovereignty prevails. That means demystifying
and eliminating financial barriers to government operations so the political
debate can focus on solving real issues (environment issues, socio-economic
issues, etc.). Fearmongering about the public debt and fiscal deficits makes for
poor political debates and policy prescriptions.
There is a view, expressed by Paul Samuelson, that if
we tell policymakers and the public that there are no financial limits to
government spending, policymakers will spend like mad; therefore, economists
need to lie to policymakers and the public (and themselves). This is nonsense.
We ought to discuss policy choices not on the basis of Noble Lies but rather on
the basis of sound and informed premises. Economists needs to make sure that
policymakers focus on resource constraints.
In addition, political constraints on government should be geared
toward improving the transparency and participatory aspects of government (e.g.
limit role of big money in elections, limit wastes, etc.). We already have a
government that passes a budget (it needs to do so for transparency and
accountability purposes), we already have an auditing process, and we already
have some (limited) democratic process, so aim at improving these aspects. MMT
proponents are not naive, we know that some politicians are self-interested, we
know that policy implementation may lead to mistakes, we know people may try to
game the system (“free riders”); however we trust that a transparent and
democratic government can (and does) get through these issues. MMT does not see
financial constraints as helping in any ways, rather they inhibit the
democratic process.
Of course, MMT proponents also have a policy agenda (Job guarantee,
financial regulation based on Minsky, etc.) because we do not see market
mechanisms as self-promoting full employment, price stability and financial
stability. As such, as you said, MMT proponents favor alternative means to
achieve these goals through direct government intervention. We don’t see the
central bank as an effective means to promote price stability. The central bank
should focus on financial stability through interest-rate stabilization and
financial regulation (an area where the Fed has not performed well).
Finally, yes independence
of the central bank is seen as a big deal but MMT disagrees for two reasons.
First, MMT emphasizes the lack of effectiveness of monetary policy in managing
the business cycle and, second, and probably more importantly, MMT notes that
central-bank independence in terms of interest-rate setting and goal settings
does not mean independence from the financial needs of the Treasury.
DA: I think it's fair to say most people want to see government
operations run smoothly, and would welcome a sober debate over the issues at
hand without the fear-mongering that some like to promote. The broad objective seems the same--the debate is more over implementation--how monetary and fiscal policy is to be coordinated--given human frailties.
Having said this, I think you go too far by asserting that
"government finances are never an issue as long as monetary sovereignty
applies." Of course, technical default on nominal debt is not an issue (we
all understand this). But SMT also recognizes the importance of economic default
on nominal debt. True, a government can always print money to satisfy its
nominal debt obligation, but if money printing dilutes the purchasing power of
money, this is a de facto default.
On a related issue, SMT asks "what are the limits to
seigniorage?" The fact that a government can print money does not give it
the power to command resources without constraint. People can (and do) find
substitutes for government money (they may also substitute out of taxed activities
into non-taxed activities). SMT treats the limits to seigniorage as a financial constraint.
Maybe MMT has a different label for this constraint? Perhaps it is related to
what I hear MMT proponents call an "inflation constraint." Maybe
one way to reconcile MMT with SMT on this score is by recognizing that SMT
usually assumes (sometimes incorrectly) that the inflation constraint is always
binding. If this is the case, a monetarily-sovereign government does have
a financial constraint, even according to MMT.
ET: Yes, ability to create a
currency does not mean ability to command resources because there may not be a
demand for the currency. That is where tax liabilities and other dues owed to
the government become important (cf. the chartalist theory of money, a
component of MMT). That’s also why taxes, monetary creation and bond issuance
are not conceptualized by MMT as alternative financing means but rather as
complementary. The government imposes a tax liability, spends by issuing the
currency necessary to pay the tax liability, then taxes and issues bonds. Spending may be inflationary
indeed and so there is an inflation constraint; but it is not a financial constraint,
it is a resource constraint.
About the “printing” of money
by government, inflation and economic default. Regarding the first two, there
is no evidence of an automatic relation between money and inflation. In a
consolidated view, government always spends by monetary creation but controls
the impact on inflation via taxes and the impact on interest rates via bond
issuance. In an unconsolidated view, the central bank routinely finances and
refinances the Treasury by helping some of the auction bidders and by
participating in the auction.
Finally, regarding economic
default, governments routinely “default” in that sense with no problems. I
don’t see that as a relevant concept unless someone can show that economic
default raises interest rates or generates rising inflation (it does not); here
again, there is no automatic link between inflation and interest rates. That
link depends on how the central bank reacts; if it does not then market
participants don’t either.
DA: Let me return to the manner in which the Fed/Treasury/Congress
are consolidated (or not) in SMT and why this matters, in your view. In some
SMT treatments, Congress decides spending and taxes, which implies a primary
deficit. It's up to the Treasury to finance that deficit, with the Fed playing
a supporting role (by determining interest rate and issuing reserves for
treasury debt). What's wrong with this approach?
ET: That goes in the
right direction with an understanding that the government really has no control
over its fiscal position. All this, which relates to the implementation of
monetary sovereignty, helps understand why the financial crowding out is not
operative, why monetary financing is not by definition inflationary, why i >
g is normal. It helps explain why the hysterical rhetoric surrounding the
public debt and deficits in nonsense. I recently wrote a piece for Challenge Magazine on that topic. Surpluses are celebrated, governments implement
austerity during a recession to “live within our means”, Social Security needs
to be fixed to avoid bankrupting it, governments need to save more, etc. All of this is incorrect.
DA: I'm not sure why you claim SMT leads to the idea of i > g.
The case i < g is perfectly consistent with SMT (see Blanchard's 2019 AEA
Presidential address, and also my posts here and here). The
correct criticism (I think) is that mainstream economists have assumed i > g
as being the empirically relevant case (it is not).
ET: That is what I meant. MMT links that to monetary sovereignty.
DA: I think that's correct. I should like to add that mainstream economists (apart from a small set of
monetary theorists) have not appreciated the role of high-grade sovereign debt
as an exchange medium in wholesale financial markets and as a global store of value, which in my view likely explains a lot of the "missing inflation." But as for
"surpluses being celebrated," you are now talking about individual
viewpoints and not SMT per se. There were plenty of calls out there
for countercyclical fiscal policy based on standard macroeconomic principles.
But I do agree virtually all mainstream economists are (perhaps overly)
concerned about "long-run fiscal sustainability." The view is that at
the end of the day, stuff has to be paid for -- and that having the ability to
print money, while granting an extra degree of flexibility, does not get around
this basic fact.
DA: I'd like to ask you about this statement you make:
In (the unconsolidated) case, the Treasury collects taxes and
issues securities before it can spend. However, federal taxes and bond
offerings also serve another highly important function that is overlooked in
standard monetary economics. Specifically, federal taxes and bond offerings
result in a drainage of funds from the banking system, and MMT carefully
analyzes the implication of this fact. From that analysis, MMT argues that
federal taxes and bond offerings are best conceptualized as devices that
maintain price and interest-rate stability, respectively (of course, the tax
structure also has some important role to play in terms of influencing
incentives and income distribution; something not disputed by MMT).
DA: Well, yes, taxes serve both as a revenue device
(permitting the government to gain control over resources that would otherwise
be in control of the private sector) and as a way to control inflation. I'm not
sure about the idea of the Treasury offering bonds for the purpose of achieving
interest-rate stability (though this may happen to some extent when the
treasury determines which maturity to offer). I don't think this is the way
things work in the U.S. today.
ET: Taxes and issuance of
treasuries drain reserves and so raise the overnight rate. Hence, on a daily
basis, a fiscal surplus raises the overnight rate and a fiscal deficit lowers
it. There has been significant Treasury-Fed coordination to smooth the impact
of taxes (and treasury spending) on the money market.
DA: Fine, but so what? We all understand
"coordination" between Fed and Treasury exists at the operational
level.
ET: I think you are too kind to other
economists and policymakers. On taxes as price-stabilizing factors, there is
indeed some similarities here. On the role of treasuries for interest-rate
stability, it does work like this today. It may not be obvious because of the
current emphasis on treasuries as Treasury's budgetary tools, but Treasury has issued securities for
other purposes than its budgetary needs. In the US, this occurred most recently during the 2008
crisis (SFP bills). In Australia, in the early 2000s, the Treasury issued
securities while running surpluses in order to promote financial stability.
DA: But even if this is not the way things actually work
(in my view, it's the Fed that stabilizes interest rates, possibly through OMOs
involving U.S. Treasuries), I'm not sure what point is being made. I think we
can all agree that monetary and fiscal policy can be thought of as being
consolidated in some manner. What would be good to know is how a specific MMT
consolidation matters (relative to other specifications) for a specific set of
questions being addressed. There is nothing in the abstract or introduction of
this paper that suggests an answer to this question.
ET: The point being made is that in a consolidated
government, tax and bond issuance lose the financial purpose
they have for the Treasury but keep their price and interest-stability purposes.
DA: In standard monetary theory, tax and bond issuance keeps
its funding purposes for the government and at the same time can be used to
influence the price-level (inflation) and interest rates. Is this wrong? I
don't think so. At some level, taxes (a vacuum cleaner sucking up money from
the private sector) must have some implications for the ability of government
to exert command over real resources in the economy. What we label this ability
(whether "funding" or ''finance" or whatever, seems
inconsequential).
ET: Ok here comes the crucial difference between financial
and real sides of the economy. In financial terms, taxes do not increase the
capacity of the government to spend, i.e. the government does not earn any
money from taxing; taxes destroy the currency. In financial terms, there is no
reason to fear a fiscal deficit; deficits are the norm, are sustainable and
help other sectors grow their financial net wealth. As such, it is not because a
government wants to spend more that it must tax more or lower spending
somewhere else. That is the PAYGO mentality. This mentality makes policymakers
think of spending and taxing in terms of how they impact the fiscal balance
instead of their impact on employment, inflation, incentives, etc. While
deficits may have negative consequences, they are not automatic. If
one takes a look at the evidence, deficits have no automatic negative impacts
on interest rates, tax rates, public-debt sustainability, or inflation.
In real terms, the necessity to increase tax rates to prevent
inflation, and so move more resources to the government, depends on the state
of the economy and the permanency of the increase in government spending relative to
the size of the economy. In an underemployed economy, the government
can spend more without raising tax rates. In a fully employed economy, shifting
resources to the government without generating inflation does require raising
tax rate and/or putting in place other measures such as rationing, price
controls, and delayed private-income payment. Here Keynes’s “How to Pay for the
War” provides the roadmap. Standard economics is full-employment economics so
opportunity costs are always present. MMT follows Kalecki, Keynes and the work
of their followers (have a look at Lavoie’s “Foundations of Post
Keynesian Economic Analysis”) and note that capitalist
economies are usually underemployment and economic growth is demand driven. Put
in a picture, the economy is usually at point a.
Put succinctly, the real constraint is conditionally relevant, the
financial constraint is irrelevant if monetary sovereignty prevails. That is
the proper way to frame the policy debates and to advise policymakers; don’t
worry about the money, worry about how spending impacts the economy.
ET: Moving to another topic, consolidation of the government brings to the forefront
forces that are operating in the current system but that are buried under
institutional complications. Namely that a fiscal deficit lowers interest rates
and treasuries issuance brings them back up, that spending must come before
taxing and treasuries issuance, that monetary financing of the government is
not intrinsically unsound and does not mean that tax and treasuries issuance
don't have to be implemented.
DA: The statement that "deficit lower
interest rates" needs considerable qualification. Among other things, it
depends on the monetary policy reaction function. As for the claim that
spending *must* come before taxes, this is not a universally valid statement
(even if it may be true in some circumstances. But even more importantly, who
cares? Mainstream theory does not suggest that monetary financing is
intrinsically unsound (seigniorage is fine, if it respects inflation ceiling).
As for money, taxes and bonds not being alternative "funding"
sources, I worry that this semantics. You can call X a "funding"
source or not -- it's just a label. The real question is: what are the
macroeconomic implications of X?
ET: Let me emphasize where I agree. Yes, evidence
shows the central role of monetary policy for the direction of interest rates,
fiscal policy is at best a very small driver. And yes, one ought to focus on
the real implications of government spending and we ought to forget about the financial implications. A fiscal
deficit is not unsustainable nor abnormal; deficits are the stylized fact of
government finances and are financially sustainable if monetary sovereignty is
present. So don’t try to frame the policy debate and set policy in terms of
household finances, bankruptcy, fixing the deficit, etc.
To conclude I see three reasons why the "taxes/bonds don't
finance the government" rhetoric is helpful:
1- It is strictly true for the federal government (i.e.
consolidation).
2- it brings to the forefront some lesser-known aspects of taxes
and treasuries issuance: impacts on money market, role of central bank in
fiscal policy, role of treasury in monetary policy.
3- It changes the narrative in terms of policy and political
economy: government does not rely on the rich to finance itself, taxes should
be set to remove the "bads" not to finance the government (e.g. one
should not set tax rates on pollution with the goal of balancing the budget but
with the goal of curbing pollution to whatever is considered appropriate, that
may lead to much higher tax rates than what is needed to balance the budget),
PAYGO is insane, one should focus on the real outcomes of government policies
not the budgetary outcomes.
DA:
1. I think this is semantics.
2. Not sure how it helps in this regard.
3. I think all of these positions are defensible without the
statement "taxes/bonds don't finance the government", so
if this is the ultimate goal (and I think it should be), perhaps we should set
aside semantic debates and focus on the real issues at hand.
ET: 1 is not semantic. I know you have in mind taxes as a
means to leave resources to the government. MMT makes a clear difference
between financial (ability to find the money) and resources constraint (ability
to get the goods and services) as explained above. The financial
constraint is highly relevant for non-monetarily sovereign governments so it
should be noted and clearly separated from the real constraint. Too many
policy discussions and decisions by policymakers operating under monetary
sovereignty are based on an inexistent inability to find money and the imagined dear financial
consequences of budgeting fiscal deficits. 2 helps to understand how monetary
sovereignty is implemented in practice. On 3, yes focus on the real issues.
DA: We agree on 3! Thank you for an interesting discussion,
Eric. There's so much more to talk about, but let's leave that for another day.
ET: You are welcome and thank you too!