The Cyclical/Structural Unemployment Debate

There's been a lot of talk these days about whether unemployment in the U.S. today is the product of "cyclical" or "structural" factors. For example, see: And he huffed...and he puffed...and he blew the structural unemployment house down!

This blustering (by the big bad blog wolf) brings back a fond memory. In the fall of 1988, I had the good fortune of being enrolled in a PhD macro class taught by  Peter Howitt. Peter had just returned from sabbatical leave (at MIT, if memory serves) and perhaps it was there that he picked up on the labor market search literature. (I should like to point out that he has a very nice paper on the subject, coauthored with Preston McAfee, published in 1987: Costly Search and Recruiting).

Anyway, it was in that class that the first learned of the "cyclical vs structural" debate. Evidently, the modern version of this debate started out with Lilien's "Sectoral Shifts and Cyclical Unemployment" paper (JPE 1982). Abraham and Katz countered with "Cyclical Unemployment: Sectoral Shifts or Aggregate Disturbances?" (JPE 1986).

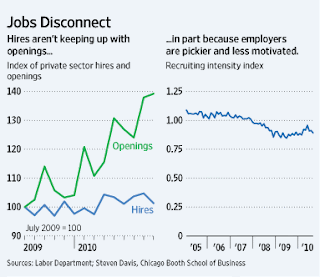
One part of the AK counterargument exploited Beveridge curve evidence. I understood their argument as saying that if structural shifts are the primary driving force, then one would expect to see a positively sloped Beveridge curve (much like what we are seeing right now in the U.S.).  In fact, the Beveridge curve is negatively sloped. Ergo, aggregate demand shocks yes; structural shifts no.

As I had just finished reading Pissarides' now-famous AER 1985 piece, I knew exactly what AK were on about. And so, why not formalize the AK hypothesis in a Pissarides-style search model? (We were all scheduled to present a short seminar in Peter's class on a research topic, and this sounded as good as any). Now, let me describe the model I wrote down and what I discovered.

The model

The model I used was a simplified version of Pissarides (AER 1985).

The economy consists of a fixed number of workers (mass normalized to unity) and a potentially "large" supply of jobs (or firms--I use the two terms interchangeably). Each job requires one worker. A firm-worker pair produce y units of output. (I assumed y to be common across matches, but allowed y to vary over time as an exogenous stochastic process).

Workers did not have any interesting decisions to make in the model. At any point in time, they were either matched with a firm or not. If they were matched, they produced output. If they were not matched, they used their fixed time endowment in search activity. Unmatched workers were "involuntarily" unemployed (because, by assumption, even menial jobs do not exist). Let u denote the unemployment rate at an arbitrary date (employment is given by n = 1 - u ).

Central to this literature is the notion of an aggregate matching function. The idea is that the aggregate recruiting intensity of firms (measured by vacancies v ) and the aggregate search intensity of workers (measured by unemployment u ) combine in some "black box" search market to produce an aggregate flow of new matches m. Formally, m = M(u,v), where M(.) was frequently specified as Cobb-Douglas (the rationale for CRS being that the ratio θ ≡ v/u displayed no secular trend in the data).

Now, Jeremy Greenwood had introduced me the year before to RBC theory. The idea there was that aggregate production possibilities, as measured by an aggregate production function y = zF(k,n) might bounce around owing to exogenous movements in aggregate productivity, z. It occurred to me that the AK hypothesis might be formalized by assuming that the efficiency of the aggregate matching function is subject to time variation owing to "structural" disturbances. That is, why could I not write m = xM(u,v), where x is analogous to the productivity shock in the RBC literature?

The idea is that a structural shock that (say) required sectoral or occupational reallocation is likely to reduce the efficiency with which matches are formed at the aggregate level (a lower x ). A lower x, in turn, would cause an "outward" (thanks, Nick) shift of the theoretical Beveridge curve, leading to the AK observation that structural shocks should induce unemployment and vacancies to move in the same direction. I was getting excited. But then, I was still young back then.

Alright then, back to the model. Following Pissarides, I denoted q ≡ m / v and p ≡ m / u as the match probabilities for vacant firms and unemployed workers, respectively. Utilizing the CRS matching technology about, we can write these match probabilities as functions of the "labor market tightness" variable θ (as well as the structural shock x, which I leave implicit). It turns out that q(θ) is a decreasing function of θ; more vacancies competing for the pool of unemployed reduces each firm's chances at making a match. Likewise, p(θ) is an increasing function of θ; more vacancies makes it easier for the unemployed to find work.

Firms and workers bargain over the output produced in a match. I assumed, for simplicity, that the wage is given by w = αy; where 0 < α < 1 is a parameter indexing the worker's bargaining power.

At the beginning of the period, the firm-worker match breaks up with probability 0 < σ < 1. Call this the separation rate. Let 0 < β < 1 denote the discount factor. If the value of a firm without a worker is normalized to zero, then the capitalized value of a firm with worker is simply the expected discounted stream of profits. If I let J denote the capital value today, and J⁺ the capital value tomorrow, then we have the following Bellman equation:

[1] J = (1 - α)y + (1 -σ)βE[J⁺ | ω]

The term E[J⁺ | ω] denotes the expected future value of firm operations, where the expectation is formed conditional on information ω.

Notice that I can embed the usual RBC assumption of persistent aggregate productivity shocks by assuming that ω = y. Or, we might model aggregate demand shocks as exogenous shifts in ω (my preferred interpretation is that these are news shocks). Absent any aggregate uncertainty, we can impose J = J⁺ and solve for the steady state capital value J^*; i.e.,

[1a] J^* = (1 - α)y / [1 - (1 - σ)β]

The next step is to figure out what determines aggregate recruiting intensity. Assume that posting a vacancy incurs the resource cost κ. Then, assuming free-entry in vacancy creation, the equilibrium labor-market tightness variable θ is determined by:

[2] q(θ)(1 -σ)βE[J⁺ | ω] = κ

The formulation above assumes that even newly created matches are subject to exogenous separation in the following period. In any case, note that since u is predetermined, condition [2] pins down equilibrium vacancies v. That is, v is a "jump variable" that responds instantaneously to any shock. If an increase in ω results in an increase in the value of a firm, for example, the effect will be to increase vacancy creation. As new vacancies come online, the probability of successfully finding a worker falls, until condition [2] is again satisfied.

Note that we can combine [1a] with [2] to determine the steady-state labor market tightness variable:

[2a] q(θ^*)(1 -σ)βJ^* = κ

Finally, we need an expression that describes the evolution of the equilibrium unemployment rate. This is given by u⁺ = u + σ(1-u) - (1-σ)p(θ)u; or

[3] u⁺ = σ + [ 1 - (1-σ)(1-p(θ)) ]u

The steady-state version of [3] is given by:

[3a] u^* = σ / [ 1 - (1-σ)(1 - p(θ^*) ]

That's it. What a beautiful little model. Note its lovely recursive structure: condition [1] determines J; given J, condition [2] determines θ; and given θ, condition [3] determines the unemployment rate.

Moreover, the model generates a nice downward sloping Beveridge curve. That is, an increase in aggregate demand (an increase in ω that increase J⁺) stimulates v, which reduces u. A structural shift that reduces matching efficiency (a reduction in x) shifts the Beveridge curve outward. Wonderful.

And so, following the RBC methodology I learned from Greenwood, I parameterized the model and calibrated the steady-state to some data. I specified the usual AR(1) process for the aggregate technology shock. And I added an AR(1) process for the match-efficiency (structural disturbance) shock. Then I simulated the model output for unemployment and vacancies under two scenarios. First, I shut down the structural disturbance, assuming only the TFP shock. And then I shut down the TFP shock, assuming only the structural disturbances.

To my surprise, both experiments generated downward sloping Beveridge curves (in the sense that unemployment and vacancies were negatively correlated). The correlation was a bit weaker under the structural shocks (something like -0.50 vs. -0.80, if I remember correctly). But the correlation was still negative! (I am going to assume that this was not the product of a coding error!)

In any case, during my class presentation, I explained the result as follows. Imagine hitting this model economy with a structural disturbance that manifests itself as a decrease in matching efficiency. In terms of condition [2], this is like a negative technology shock to the match probability q(θ). On impact, the unemployment rate remains fixed; hence, all the adjustment must be absorbed by the "jump" variable, vacancies. And if firms now find it harder to match, vacancies are going to jump down. The contraction in job availability then manifests itself as a higher (future) unemployment rate. Could the logic supplied by Abraham and Katz in refuting Lilien's hypothesis be wrong? Maybe.

Lessons

I don't want to make too much out of this simple model. One reason not to like it for the question at hand is that it is only a one-sector economy (though, my classmate, Paul Storer, eventually produced and estimated a very nice two-sector model here). 

The point here is not to say who is right and who is wrong. Maybe the Abraham and Katz hypothesis is correct...or maybe it is not. I don't know. The important thing, in my mind, is what I learned from this experience; namely, to be very careful in accepting too quickly (or too uncritically) predictive statements based on informal stories.

Beveridge Curves for 4 U.S. Regions (JOLTS)

Regarding my earlier post, a few people have pointed out that the measure of job vacancies I employed was based on newspaper advertisements. To the extent that there has been a shift in advertising away from print to online media, the Beveridge curves I plotted earlier may be distorted.

Evidently, the conference board has some measure of online job advertisements, available (I think) for only since 2005 or so. My RA reports that they want $20K for the data. Uh...sure. I'll see what I can do about this.

But in the meantime, I provide plots of regional Beveridge curves using JOLTS data which, unfortunately, is available only for the past decade. I do this first the conventional way, plotting vacancies against unemployment. But because I am no fan of unemployment measures (half of the flow into employment comes from out of the labor force), I also plot the BC my preferred way; that is, with vacancies plotted against the employment ratio.

 

Beveridge Curves for 36 U.S. Cities

A lot of talk about Beveridge curves these days. Most (all?) discussions revolve around national level data; see, for example, here: A Curious Unemployment Picture Gets More Curious. I thought it might be interesting to look at city-level data and over a longer horizon.

The following charts were constructed by Constanza Liborio (my faithful RA). To ease cross-city comparisons, all charts are of exactly the same dimension. The help wanted index (HWI) is from the Conference Board Help Wanted Index (1987=100). Constanza divided the city-level HWI by city-level employment, and then normalized 1987=1. The city-level unemployment rate data is from the BLS.

We have data for most cities ranging from 1984-2009 (some include 2010). The 1980s are colored purple; the 1990s are colored red; and the 2000s are colored green. (You should be able to enlarge the diagrams by clicking on them).

One thing that struck me was how steeply sloped the "long run" Beveridge curve appears to be across many cities. Or, if you're one who likes to imagine relatively flat BCs shifting over time (a la here: A Classroom Lesson: The Phillips Curve), then this evidence appears to suggest that something "structural" has been in play since the mid 1980s. Take a look, for example, at Cleveland and Miami. The unemployment rates in those cities are now about the same as they were in the mid 1980s and mid 1990s; even though recruiting intensity has dropped to the floor.

And take a look at poor Detroit. Here, one is tempted to say that low recruiting intensity is responsible for high unemployment (the classic BC statement). But as Cleveland and other cities demonstrate, unemployment can be high for reasons that appear independent of recruiting intensity.

Please feel free to share your impressions of this data.

Old Dogs, New Tricks

Came across this story today: Unemployed Find Old Jobs Now Require More Skills. According to this article,

The jobs crisis has brought an unwelcome discovery for many unemployed Americans: job openings in their old fields exist. Yet they no longer qualify for them.

Evidently, companies are asking more of their new recruits; they want workers with a broader range of skills. Tech companies, for example, are increasingly combining business analyst and systems analyst positions. Workers laid off from these positions during the recession frequently do not have the combined skill set that employers are now looking for.

What has changed? Why are companies now looking for workers with broader skill sets? I haven't really thought about it that much, but here a couple of (speculative) ideas.

One hypothesis is that these new demands reflect an ability on the part of firms to squeeze more output from workers, whose bargaining positions are weakened when unemployment is high. If this is true, then I suppose we should expect to see a similar pattern in past recessions. Moreover, we should (I think) expect the opposite to hold during booms. Do we, in fact, observe firms asking for narrower skill sets during economic expansions?

(It would be interesting to know (the article does not mention) whether workers with expanded skill sets are command higher wages, relative to the workers they replaced. Does anyone happen to know?)

Another hypothesis is that these new demands reflect the efficient outcome of a new reality, brought about by new technologies, or other changes in the economic environment. For a given environment, I imagine that there is an optimal skill set, or division of labor, within each firm (or line of business). It makes little sense to have every worker perform every conceivable task, or to hire a separate worker for each little task. It may or may not make sense to have the optimal mix of tasks per worker vary over the business cycle (one's view on this is likely to depend on what one believes is driving the cycle and what sort of mechanisms govern resource allocation in the labor market).

My guess is that secular developments (technological change) might be driving the demand for broader skill sets, and that these secular developments are interacting with separate cyclical developments to deliver the observations that are reported in the article. If this is true, then we should likely have observed these "new" demands growing even in the last expansion. I wonder what data is available to either support or refute this hypothesis.

In any case, judging by the evidence highlighted in this article, it appears that jobs are available and that qualified workers are in short supply. It's not immediately clear what this implies about how the rate of unemployment is likely to evolve in the foreseeable future. To the extent that unemployment workers recognize the need to upgrade their skills, they may temporarily dropout of the labor market to do so. The unemployment rate in this case is likely to drop in the near horizon. To the extent that skill upgrades are not viewed as necessary, unemployed workers may continue to search until they find a good job match, or until their reservation wages decline to the point of desperation (they will take any crappy job that helps pay the bills). In this latter scenario, unemployment may remain persistently high in the near horizon.

Several other questions spring to mind, but I was told by a loyal reader that I should shorten my posts, so I'll stop here! Feel free to share your thoughts.

Update 10/12/2010

One of my readers writes:

There was also research published today by Goldman Sachs on the search/match problem in the labor market.  Their approach was to look at data from a 'small business' survey conducted by the National Federation for Independent Businesses.  They looked at proportion of businesses reporting "no qualified applicants for job openings" and synthetically extended the series back in time by using the relationship between that series and the proportion of businesses reporting "quality of labor as most important problem".  They concluded that "the increase in unemployment has pushed firms’ difficulties in filling vacancies to record low levels", and that this is consistent with weak aggregate demand rather than a search/match problem.

I also thank this reader for directing me to the following related article from the WSJ: Unfilled Openings Frustrate Jobless. The following graph from the article shows an explosion in job openings since 2009, but very little movement in actual hires.

This data appears consistent with the theme in the article cited originally in this post. Employers appear to be choosier at this stage of the cycle; they are asking more from new recruits (e.g., broader skill sets). Of course, it is possible that workers are also exhibiting a high degree of choosiness (keeping their reservation wages high). As the article suggests, this may be because of extended unemployment benefits and/or mortgage troubles and poor credit scores that make it difficult for people to move for work.
As usual, the reasons underlying this apparent increase in choosiness varies.

Some companies complain that when they do try to hire, they have a hard time finding the right people.

Statements like these are not very informative. I know from my own experience in the construction sector that companies always have a hard time finding the "right kind of people." In fact, this problem is likely worse in a boom period (which is why firms typically get less choosy about worker quality in a tight labor market). The question is whether this problem is now more severe at this point in the cycle, relative to similar points in past cycles.
The following executive probably speaks for a lot companies:

At Leggett & Platt Inc., which makes metal parts for bedding and other purposes, Chief Executive David Haffner says his company remains hesitant about anykind of expansion, because it's not clear to what degree demand will snap back. But when it does hire, it's taking more time. "With more experienced talent on the market in these challenging times, we are utilizing a more rigorous screening and interviewing protocol," says Mr. Haffner. "We feel it is crucial to add 'top graded' talent."

I find the claim of "more experienced talent on the market" these days. My earlier post In Praise of Older Women suggests that the aged are in the midst of an employment boom (so old dogs are apparently pretty good at picking up new tricks!)

The quote above also emphasizes a lack of "demand." The question here is what's holding back "demand?" There is clearly a "lack of confidence" in the business sector relating to forces that are likely to impinge on future demand conditions. Has there been a change in economic fundamentals, leading to a bout of "rational pessimism?" Or is the lack of demand simply a product of some collectively irrational (but individually rational) psychological force? The appropriate policy response is likely to depend on the answer to these questions.

In Praise of Older Women

By all accounts, the U.S. employment picture looks bad. But what do we mean by "bad?" The most common way to demonstrate how bad it is, is via a diagram like this (source):

 

See also here. These displays take the level of employment at its cyclical peak and normalize it to zero. This is done for several earlier episodes, and then the evolution of employment is tracked from the onset of each recession. And, well, the current episode looks bad.

Diagrams like the one above are interesting. But I think they need to be read with some caution. You may not even know it, but the diagram has planted an idea in your head. The idea is that the data are stationary, and that reversion to the mean is desirable. It is sometimes useful to look at the broader picture; and this is what I propose to do here.

Here is a plot of the U.S. employment ratio (employment divided by population) over a longer horizon than is normally considered (1948-2010):

The first thing that should strike you is that the employment ratio does not appear to be stationary, at least, over this sample period. It seems to be roughly stationary in the first half of the sample, but then it grows steadily, reaching a peak in the late 1990s. Since that time, it has (arguably) been on a downward trend. It is possible that the recent cyclical decline is exacerbated by this downward trend (and may have contributed to the recent jobless recovery phenomena).

If the trend is indeed heading downward, in what sense should policymakers desire a return of employment to its earlier cyclical peak?  Do we know what the "natural" rate of employment is?

Perhaps the recent downward trend is not the only thing that needs explaining. We might also puzzle over the employment boom that seems to have begun in the mid 1970s. The following figure is revealing.

What we see here is that the employment ratio for men was in secular decline until the early 1980s. The employment ratio for women, in contrast, has been increasing steadily up until 2000. So the large increase in total employment is accounted for by female employment decisions. But since 2000, the employment ratio seems to be on a slow downward trend for both sexes, until falling sharply (again, for both sexes) in the recent recession.

Let me now slice the data up into finer categories. Here is the employment ratio for men by age:

What this suggests is that the secular decline in male employment early on in the sample was attributable largely to the employment choices of older men. The trend seems to have reversed itself some time in the early 1990s. Offsetting this rise is a decline in the employment of young men. The recent recession seems to have hit young men particularly hard; the employment ratio for older men hardly budged at all.

Here is what the employment ratio looks like for women across age groups:

What this suggests is that the recent secular decline in female employment is attributable largely to the behavior of young women (are all going to college?). But what I find very interesting here are the labor supply choices of older women.  In particular, their employment continued to expand even throughout the recent recession!

I am not sure what is driving this behavior. I do find it interesting, however, that a large negative aggregate demand shock seems not to have had much of an impact on the demand for goods and services produced in "old age" sector of the economy.

Theory Ahead of Language in the Economics of Unemployment

The language used to describe economic phenomena is frequently laced with economic theory, even if we do not realize it.  Labelling a measure of GDP as "demand," for example, betrays an underlying theory. The same is true of a lot of the language that surrounds discussion of unemployment these days.

How is unemployment defined? Well, it depends. A lot of people seem to have their own pet definitions. That's fine. But let's stick to the way it is defined officially, by the people who collect these statistics; see How the  Government Measures Unemployment. (For a list of alternative measures, see here).

So this is how it works. You are asked in a survey whether you have done any paid work in the previous four weeks. If you answer yes, then you are counted as employed. If you answer no, then you are nonemployed.

If you are nonemployed, you are asked another question: Have you been doing anything in the past four weeks to find work (and if so, what)? If your job search activity is judged to be sufficiently "active," then you are counted as unemployed; otherwise, you are counted as a nonparticipant.
 
One thing that should strike you about this procedure is that workers are never asked whether they are unemployed or not. It's not up to them to decide.

Nonemployment consists of both unemployment and nonparticipation. What is the distinguishing characteristic between unemployment and nonparticipation?  Clearly, it is not joblessness. The distinguishing characteristic is active job search.  (The only exception to this appears to be the small number of workers on temporary layoff).

I think it is important to recognize this distinction and what it might mean for how we go about thinking about unemployment (and what might be done about it). A lot of people (including macroeconomists writing introductory textbooks) are fond of equating unemployment with idleness. But is it right (that is, might it be misleading) to equate active job search with idleness?

One frequently reads that "unemployment represents wasted resources." But if  job search is an information-gathering activity, designed  to locate a high quality job match, in what sense does such an activity necessarily constitute wasted resources? (Does the existence of single people in the marriage market also represent wasted resources?) If the unemployment rate were to suddenly plummet because a large number of workers aborted their job search activity--accepting crappy jobs, or exiting the labor force--is this a reason to celebrate? Should the Fed, in this event, breathe a sigh of relief?
 
To the extent that unemployment (as measured in the data) represents job search activity, it seems to me that the fundamental cause of unemployment is a matching friction. Evidently, people do not know the "location" (broadly defined to include, sector, occupation, etc.) of their best job match; and so, it makes sense to go looking for your "soulmate," rather than matching with the first thing that comes along. This suggests that a theory of unemployment should model these matching frictions explicitly. A sticky wage is not going to do the trick. A sticky wage may depress employment; if so, it leads only to nonemployment, not unemployment (there is no reason to search if you know that jobs are not available).

Thinking in this manner is likely to influence our views about policies designed to "cure" unemployment. For example, it suggests that extending UI benefits during a recession may be part of a desirable policy. The idea here is to encourage unemployment (job search activity); that is, to help people find jobs that match their skills (and to smooth their consumption over difficult times). On the other hand, it leads to some scepticism over the idea of the government simply "creating jobs" in a recession. It may not be that easy--we need the "right kind" of jobs--jobs that are well-tailored to individual skills. Perhaps the market is a better judge of which skills are needed and which are not.

Anyway, I could talk a long time about this and related labor market issues. But instead, I think it might be better to point you to a paper that does the talking for me. The article is by Richard Rogerson (recently moved to Princeton) and is called Theory Ahead of Language in the Economics of Unemployment (JEP, 1997). Here is an excerpt, to whet your appetite:

One unemployment concept that macroeconomists have used extensively is the natural rate of unemployment. In a search of the literature, I came across the following uses or definitions of this term. Blanchard and Fischer (1989), in their graduate macroeconomics textbook, first equate the natural rate of unemployment to the average rate of unemployment (p. 349), only to later equate it to the equilibrium rate of unemployment (p. 545). In their chapter of the Handbook of Labor Economics devoted to the natural rate, Johnson and Layard (1986, p. 921) write: ‘‘In this chapter we deal with unemployment in the long run. We do not bother about the movement of unemployment over the cycle, but only with its average level. In other words, we are looking at what we call the equilibrium unemployment rate. . . . This is what Friedman called the ‘natural unemployment rate’. . . .’’ Also in the Handbook of Labor Economics, Hall and Lilien (1986, p. 1021) write: ‘‘The natural rate is the normal unemployment rate that results from this process of labor allocation when workers and firms correctly perceive the levels and rates of change of price and wages.’’ Lilien (1982, p. 777) had earlier written, ‘‘Because it takes time for separated workers to be matched to jobs, some positive level of unemployment will always exist. Economists have long recognized this fact and have labelled this necessary quantity of unemployment the frictional, natural or equilibrium unemployment rate.’’ In his undergraduate textbook, Mankiw (1994) defines the natural rate of unemployment to be the steady state rate of unemployment, whereas in their undergraduate text, Auerbach and Kotlikoff (1995, p. 426) refer to the natural rate of unemployment as the ‘‘lowest sustainable rate of unemployment.’’ Bean (1994) defined the natural rate to be the equilibrium rate, whereas Christiano defines the natural rate to be the trend component of unemployment generated by the Hodrick-Prescott filter. Clark and Summers (1979) suggest that it is the efficient rate of unemployment, and Hahn (1980) defines the natural rate of unemployment to be unemployment at full employment.

If transitivity is assumed to hold, then the above list of quotations would tell us something like: long run = frictional = average = equilibrium = normal = full employment = necessary = steady state = lowest sustainable = efficient = Hodrick-Prescott trend = natural. It would seem doubtful that any concept that is sufficiently ambiguous as to promote this many different uses can be helpful in guiding scientific inquiry. I am by no means the first to question the clarity of this concept. Solow (1986, p. S24) has written, ‘‘[I]t is not clear what we are talking about when we talk about the natural rate.’’

In a larger context, the natural rate of unemployment was only one of many terms that were introduced supposedly to clarify key issues and lead the search for a theory of unemployment. Primary among the other terms were several decompositions of measured unemployment; there was equilibrium and disequilibrium unemployment, voluntary and involuntary unemployment, and frictional and cyclical unemployment. There was also the notion of full employment unemployment. Milton Friedman (1968) was adding to this list in his presidential address to the American Economic Association when he introduced the concept of the natural rate of unemployment. Much of this ‘‘language of unemployment’’ continues to be used today. Is this because these terms have turned out to be the precise and powerful concepts that facilitate clear communication and allow issues to be defined sharply? In this essay, I will argue that they are not.

The full article is available here: Theory Ahead of Language in the Economics of Unemployment.