The Beveridge curve (BC) refers to the relationship between job vacancies and unemployment. There are really two types of BCs: one empirical, and one theoretical. The empirical BC is simply a scatterplot of vacancy and unemployment data. Think of data as the entrails of a gutted animal. The theoretical BC is an interpretation of those entrails, as divined by an economic haruspex.
The empirical BC is usually negatively sloped. Except for when it isn't. (You know how it is.)
The theoretical BC is a very intuitive creature. If some measure of general business conditions improve, especially in terms of economic outlook, businesses will generally want to expand their investments. And this includes investment in the form of replenishments to their labor force. If the labor market is subject to search frictions, the hiring process will take time. But an increase in job openings will generally make it easier for unemployed workers to find a job, so we would expect unemployment to decline as job vacancies rise.
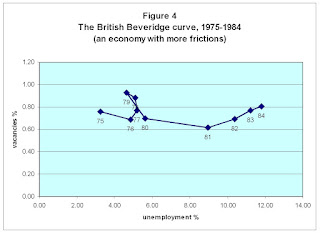
Sometimes, however, the BC appears to "shift" its position (e.g., if the BC looks like a shotgun blast). These apparent shifts are sometimes interpreted to be the consequence of shocks that somehow lead to increased search frictions (let me label these "structural" shocks). In his fine Nobel prize lecture, Christopher Pissarides gave the example of Brittain 1975-84:
Usually though, the BC has a sharper negative slope. This was certainly the case in the United States; at least, until recently. Here is a plot of the U.S. BC using JOLTS data. Both job openings and unemployment are divided by a measure of population (16+ civilian). The dots represent the empirical BC and the solid line represents a theoretical BC.
A fairly conventional interpretation of the pattern above is that the U.S. experienced a cyclically-induced increase in unemployment; at least, approximately up until the recession was formally declared ended. These are the blue dots (lying close to that BC line I am forcing into your brain). Since then, something screwy appears to have happened in the labor market. There is evidence of increased recruiting activity, but no evidence of declining unemployment (the red dots).
Is this evidence of some greater difficulty in matching unemployed workers to available jobs? Did the recent recession leave us with some "structural" problems? If so, can we identify precisely what these "structural" problems are, and what--if anything--might be done about it? These are just some of the questions people are asking theses days.
Unfortunately, I'm not presently able to answer these questions. What I offer, instead, is some speculation on another question that has been floating in my mind lately. In particular, is the pattern of the U.S. BC plotted necessarily inconsistent with the notion that "structural" shocks have afflicted the labor market throughout the recent recession?
It was Steve Williamson's blog post
here that got me thinking about this. Underlying much of the modern theory of search in the labor market is the Phelps/Pissarides aggregate matching technology:
[1] ht = xtM(vt,ut)
where
h denotes hires,
v denotes job openings (vacancies), and
u denotes unemployment. For quantitative applications,
M(.) is usually specified to be Cobb-Douglas; e.g.,
M(v,u) = v0.5u0.5. The
x parameter corresponds to the TFP parameter in a standard aggregate production function. Following Steve, I use the JOLTS data to compute the matching function "Solow residual:"
[2] log(xt) = log(ht) - 0.5log(vt) - 0.5log(ut)
And here is what I get:
The red dots depict TFP from December 2007 (the official start of the recession) onward to October 2010.
According to the plot above, events beginning with the recession have reduced matching function efficiency by about 20%. That's a big drop. But what does it mean? It's important not to get too carried away with this result. In particular, we have all the usual measurement problems to contend with when constructing TFP measures. For example, much or perhaps even most of the decline in measured TFP may be the consequence of (unmeasured) reductions in search intensity.
On the other hand, there does not appear to be any good reason to simply dismiss the result as evidence of increased search frictions. We just lived through an episode that tore apart many ongoing relationships. Picking up the pieces and putting them back together again (possibly in new and more productive ways--re: Schumpeter's creative destruction) may be a bit more difficult this time around. Ultimately, I think we will need to examine the microdata to assess the "disruptiveness" of the recession. Perhaps a study along the lines of
Rogerson and Loungani (JME 1989)--who look at PSID data--might shed some light on the matter.
But until then, if we take the measured TFP data seriously (and, again, I emphasize the caveats), might this warrant reinterpreting the U.S. BC in the following way?
The red dots represent the empirical BC since the beginning of the recession (Dec 2007); the time when the estimated matching function TFP appears to weaken.
It is interesting, I think, to examine this interpretation in the light of a simple labor market search model. In an earlier post, I argued that a negatively sloped BC is not inconsistent with a sequence of shocks that deteriorate matching efficiency; see
here. Let me show you what I mean, via a simple example (that restricts attention to steady-states).
There is a cyclical variable, labeled
y. This denotes the output produced by a job-worker pair. I assume a "fair share" bargaining rule that divides this output into wage and profit components. A firm's flow profit is given by the share
ξy. The present value of this profit flow is denoted
J(y). This value is procyclical; i.e., it will increase when the cyclical variable
y increases.
If a firm wants to open a job vacancy, it must bear a cost
κ. It is successful in finding an unemployed worker with probability
xq(θ); where
θ = v/u is the "labor market tightness" variable, and where
q(.)=M(.)/v. If the new hire starts work next period, the expected present value of posting a vacancy is
xq(θ)βJ(y). The following zero-profit condition determines the equilibrium labor market tightness:
[3] xq(θ)βJ(y) = κ
Condition [3] determines
θ(y,x). It is easy to show that
θ is increasing in the "cyclical" variable
y and the "structural" variable
x.
Finally, there is a stock-flow equation that determines the equilibrium unemployment rate:
u = σ / (σ + xp(θ)); where
σ is an exogenous match separation parameter (job destruction rate).
I parameterize this simple model and compute the equilibrium vacancy-unemployment combinations under two scenarios (GAUSS code available on request). First, I vary the "cyclical" variable
y 15% above and below its mean value, holding
x fixed. Then, I hold
y fixed at its mean value and vary the "structural" variable
x 15% above and below its mean. And here is what I get:
What is interesting here is that a permanent decrease in the match efficiency parameter
x leads to a permanent decline in job creation and permanent increase in unemployment (of course, I am not suggesting that these "structural" shocks are in any way permanent in reality). I think it was
Abraham and Katz (JPE 1986) who led many (including myself) to believe that structural changes should lead to a positively-sloped BC. Of course, they did not have an explicit model. According to this simple model, they appear to be wrong. We may at least conclude that they are not necessarily correct.
In short, one reason why job openings may have declined is because it is generally more difficult for firms to find the right worker. Indeed, given how circumstances may have changed since the recession, firms may not--as of yet--even know what type of skill set constitutes the best hiring investment. Until this uncertainty in the match-making process sorts itself out, it may make sense to recruit less intensively.