Low interest rate policy and secular stagnation

Nick Rowe's post on upward-sloping IS curves motivates today's musings. I'm sorry, but what follows is a tad on the wonkish side. It's intended mainly to promote a conversation with Nick. (You can look in if you want, but I'm sure most of you have better things to do on Christmas Eve!).

Consider the Solow growth model. Output (the real GDP) is produced with capital (K) and labor (N) according to a neoclassical aggregate production function Y = F(K,N).

Define y = Y/N (output per worker) and k = K/N (capital-labor ratio). Define f(k) = F(K/N,1). Then y = f(k). That is, output per worker is an increasing function of capital per worker.

If capital and labor are exchanged on competitive markets, then factor prices are equated to their respective marginal products. Let (w,r) denote the real wage and the real rental rate, respectively. Let 0 < a < 1 denote capital's share of income. Then,

[1] w = (1 - a)f(k) and r = af(k)/k

That is, the real wage is an increasing function of the capital-labor ratio (since labor becomes relatively scarce). The real rental rate for capital services is a decreasing function of the capital-labor ratio (since capital becomes relatively abundant).

Now, consider an economy populated by two-period-lived overlapping generations. People enter the economy as youngsters, they become old, and then they exit the economy. The population of young people remains fixed at N over time t = 0,1,2,... The young are each endowed with one unit of labor, which they supply inelastically at the going wage. Hence, N represents labor supply. The young save all their income and consume only when they are old. Saving is used to finance investment, which adds to the future stock of productive capital. For simplicity, assume that capital depreciates fully after it is used in production. (None of the results below are sensitive to these simplifying assumptions).

Since a young person saves his entire wage, the capital stock (per worker) evolves over time as follows:

[2] k(t+1) = (1 - a)f(k(t)) for t = 0,1,2,... with k(0) > 0 given (as an initial condition).

The transition dynamics are such that k(t) converges monotonically to a steady-state satisfying k* = (1 - a)f(k*).

The real interest rate at date t in this model is equal to the future (t+1) marginal product of capital (which is proportional to the average product of capital), R(t) = af(k(t+1)) = af((1 -a)y(t) ) / ((1-a)y(t) ).

The IS curve in this model is defined as the locus of real interest rates and output consistent with goods-market-clearing. In the present context:

[3] R(t) = af( (1-a)y(t) )/( (1-a)y(t) ).

Equation [3] describes a conventional downward-sloping IS curve. A higher level of income (because of more abundant capital) increases desired saving, which puts downward pressure on the real interest rate. Conversely, an increase in the real interest rate reduces aggregate demand.

Now, let's consider one of Nick's experiments. Begin in a steady state. Nick considers an exogenous 10% increase in the capital stock. I'll do the opposite experiment and consider a 10% decline.

The capital-labor ratio is now lower. From [1], the effect is to lower the real wage and increase the rental rate. From its depressed level, the real wage increases monotonically back to its steady-state level. From its elevated level, the rental rate declines back to its steady-state level. The real interest rate, in turn, jumps up and then declines back to its steady-state level.

In a competitive economy, these price adjustments reflect the underlying fundamentals. The shock renders capital scarce. Less capital depresses the demand for labor, which is reflected in a lower real wage. Capital scarcity means the the return to rebuilding the capital stock is high. As saving flows into capital spending, the scarcity diminishes, and the real interest rate falls back to normal levels.

Next, to follow Nick's thought experiment in a slightly different way, suppose that a central bank tries to keep the real interest rate low in the face of the shock just described above. In fact, suppose that the central can manage to fix the real rental rate (hence the real interest rate) at its initial steady-state level forever.

If r(t) = r* forever, then by [1] the capital-labor ratio must remain fixed for all t > 1.

An implication of this policy is that the real wage will not fall. It's not that it cannot fall (it would fall if the real interest rate was permitted to rise). The real wage needs to fall, temporarily, to maintain full employment. But because it will not fall, then something else has to give. The level of employment must fall. Since k* = K/N is fixed and since K falls by 10%, it follows that N must fall by 10% as well. The central bank's refusal to permit the real interest rate to rise has led to an increase in unemployment (instead of a decrease in the real wage).

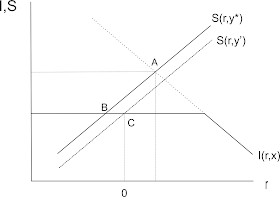
But things are even worse than they seem. While a shock that evaporates a part of the capital stock is eventually replenished when factor prices are market-determined, the same is not true when either the real interest rate or the real wage is fixed. In a post I wrote earlier (here), I considered a fixed real wage. But Nick's column made me realize that the same result holds if we fix the interest rate instead. A "low interest rate policy" in this case leads to "secular stagnation" (the level of output and employment is lower than it should be) as depicted in the following diagram:

One way to read this result is that it vindicates Bill Gross' idea that artificially low interest rate policy constitutes a form of "financial repression" inhibiting the U.S. recovery (I criticize his views here.)

How seriously to take this result? I'm not so sure. A lot depends on the nature of the shock that is imagined to have afflicted the economy. In the experiment considered above, I just wiped out a fraction of the economy's capital stock--like a hurricane, or nuclear bomb. A more generous interpretation is that the shock stands in for an event that evaporates a fraction of the value of existing capital (not necessarily its physical quantity). People do not become any more pessimistic in the model as a result of the shock, which is why the economy transitions back to its initial steady-state when the price-system is left unencumbered. A depressed economic outlook, on the other hand, would serve to reduce real interest rates, not increase them as in the experiment above--and that sort of scenario would provide more justification for low-interest policy.

Merry Christmas, everyone.

Schumpeterian growth and secular stagnation

What is secular stagnation? The "secular" part suggests something that's persistent--in the order of decades (as opposed to the 2-5 year frequency usually associated with a business "cycle."). The "stagnation" part suggests a measure of under-performance. But what measure? Are we talking about lower than average growth in employment and incomes? Or are we talking about depressed levels, instead of depressed growth rates? Are we talking about both? Getting this straight makes a difference in how we want to approach thinking about the phenomenon in question.

In what follows, I'll take the view that secular stagnation refers to prolonged episodes in which growth in real per capita income (GDP) is lower than its long-run average.

Most economists agree that long-run growth in material living standards (real per capita income or consumption) is the product of technological progress. Contemporary business cycle models (at least, those used for monetary policy) assume that technological progress occurs more or less in a straight line. This abstraction may be fine for some purposes, but I never much liked it myself. As a PhD student, I was influenced by Schumpeter's 1939 masterpiece Business Cycles.

Schumpeter (1939) emphasized that there is no God-given reason to expect growth to occur in a straight line. Research and development, and the process of learning in general, can be expected to generate innovations of random sizes and at random intervals. Moreover, any given innovation takes time to diffuse. Economy-wide productivity does not jump instantaneously with the arrival of the internet. I like this quote from his book:

 ‘‘Considerations of this type [the difficulty of coping with new with new things] entail the consequence that whenever a new production function has been set up successfully and the trade beholds the new thing done and its major problems solved, it becomes easier for other people to do the same thing and even improve upon it. In fact, they are driven to copying it if they can, and some people will do so forthwith. Hence, it follows w that innovations do not remain isolated events, and are not evenly distributed in time, but that on the contrary they tend to cluster, to come about in bunches, simply because first some, and then most, firms follow in the wake of successful innovation.’’ [p. 100]

It was this passage that led me to think of a model in which technological innovation drove growth but in a manner that was uneven because of diffusion lags. The notion that a new general purpose technology might spread like a contagion to generate the classic S-shaped diffusion pattern in GDP seemed like a very interesting hypothesis to investigate.

I was also influenced by Zvi Griliches' famous empirical investigation of the diffusion of hybrid corn in the United States:

In my paper (actually, the second chapter of my PhD thesis, published in 1998 with Glenn MacDonald) I saw this:

And so Glenn and I built a dynamic general equilibrium model where firms were motivated to innovate and imitate superior technologies. We estimated parameters so that the model reproduced the smooth but undulating path of GDP depicted in the figure above. I think I see these patterns in more recent TFP data as well (source):

According to this interpretation, episodes of secular stagnation are largely an inevitable byproduct of the process of technological development and growth. Accepting such an interpretation does not, in itself, have any implications for the desirability of policy interventions. But it does call into question the efficacy of certain types of interventions. In particular, do we really believe that more QE will spur future economic growth? Or should policy attention be directed elsewhere?

Now, one might object, as Larry Summers does here, that "If the dominant shock were slower productivity one might expect to see an increase in inflation." The type of reasoning that underpins this view is the simple Quantity Theory of Money equation: PY=VM. Ceteris paribus (holding MV fixed) a decrease in real income Y should induce an increase in the price level P. Maybe the 1970s provides the empirical basis for this view.

But there is no theoretical reason to believe that productivity slowdowns, or indeed, expected productivity slowdowns, should be inflationary. It's very easy to demonstrate, in fact, that "bad news" in the form of a slowdown in productivity leading to depressed expectations over the net return to capital spending can cause a "flight to safety" to government debt instruments (including money). The effect of such portfolio substitution is to depress bond yields and the price-level (see here and here for example).  But even apart from these effects, the behavior of inflation depends critically on the nature of monetary and fiscal policy.

The Neo-Fisherian Proposition

The Neo-Fisherian proposition is that a persistent policy-induced increase in short-term nominal interest rates will lead to higher inflation in the long-run. John Cochrane, one of the main proponents of this view (along with my colleague, Steve Williamson) discusses the idea here. Visually, the proposition asserts something like this:

Of course, the conventional view is that raising the policy interest rate will cause inflation to go down, not up. The idea that the opposite might be true is evidently something to be ridiculed.

Wonder why world is in a mess? Neo Fisherians: ”lowering rates causes inflation to slow down & raising rates causes inflation to speed up."

— Ann Pettifor (@AnnPettifor) December 15, 2015

I can't help but think that Pettifor's view on the proposition was formed without first trying to understand it's underlying logic (but I could be wrong). Also note that the proposition is not inconsistent a higher interest rate leading to lower inflation in the short-run.

Why do people generally feel uncomfortable with the Neo-Fisherian proposition? I think that fellow Canuck Grep Ip of the WSJ gets at one reason here where he writes:

Neo-Fisherism has theoretical elegance but lacks intuitive logic. At its heart, neo-Fisherism says there is, somewhere, a fixed real rate that drives what the public expects inflation to be. Yet few people–even those who know what real rates are–have a firm view of what they should be. Their expectations of inflation are more likely to depend on past inflation, central bank or private forecasts, and the state of the economy. These expectations of inflation will then drive the returns they expect on saving and investment, not vice-versa.

The uncomfortable part is that despite this apparent lack of intuition underlying the proposition, it appears consistent with recent experience:

However, in a recent column, David Beckworth questions whether the proposition is consistent with what is happening in Japan. This led me to ask him:

@dandolfa The one that says raising interest rates is necessary to raise inflation. This is being violated in Japan. pic.twitter.com/vrOiJV6uUh

— David Beckworth (@DavidBeckworth) December 15, 2015

Now, it might seem strange to some of you that I asked him which Neo-Fisherian theory he was referring to, but I did so because there seem to be two different strains. But before I get to that, it's worth emphasizing that the proposition does not state that raising interest rates is necessary to raise inflation. (I stated the proposition above, go read it again if you have to.)

The first strain of the theory seems to rely entirely on rational expectations and the Fisher equation (without any reference to central bank balance sheets or the conduct of fiscal policy). The way this thinking goes is that the Fisher equation is just a no-arbitrage-condition. (No-arbitrage-conditions are compelling economic restrictions because if they did not hold, traders could make infinite riskless profits.) If a central bank raises the nominal interest rate, then for a given real rate of interest, the expected inflation rate must rise (else traders will be making infinite profits). This seems to be the interpretation favored by Stephanie Schmitt-Grohe and Martin Uribe (see my discussion here).

Personally, I am not sold on this interpretation. I prefer the second strain of the theory, which is related more to the fiscal theory of the price-level (as the name suggests, the theory emphasizes the role of fiscal policy in helping to determine inflation).  According to this interpretation, the proposition that "a persistent policy-induced increase in short-term nominal interest rates will lead to higher inflation in the long-run" must be qualified with the condition that the fiscal authority passively accommodate the monetary authority's policy decision (see my column here: A Dirty Little Secret.)

Intuitively, think of the following thought experiment. The Fed raises its policy rate and its widely expected to remain at this elevated level for the foreseeable future. The effect of this policy is to increase the carrying cost of debt for the government. Assume that the government services this higher debt burden not by cutting expenditures or increasing taxes, but by increasing the rate of growth of its nominal debt. Essentially, the government is printing "money" to finance interest payments on its debt. Then (assuming a constant long-run money-to-debt ratio) the money supply must start growing at this higher rate. Suppose that people generally understand this (a big supposition, I know). Then, people should revise their inflation expectations upward (and actual inflation should result, not because of inflation expectations, but because the monetary and fiscal authorities are printing nominal liabilities at a more rapid pace to finance the higher interest cost).

I'm pretty sure that David and others understand the proposition when it is framed in this manner. Whether this is what actually transpires is, of course, anybody's guess (consider this case study for Brazil 1975-1985). It's really  hard to forecast precisely how the fiscal authority (Congress) might react to higher interest rates. I do find it interesting, however, that fellow Twitterer Matt Yglesias noticed the following:

Impressive how quickly congress has stopped caring about the deficit even as the end of ZIRP means it actually might make sense to care.

— Matthew Yglesias (@mattyglesias) December 16, 2015

Impressive indeed. But if interest rates on U.S. treasury debt continue to rise, the debt-service problem will make the headlines soon enough. The debate will then turn to whether the U.S. should cut G and increase T (austerity) or permit more rapid debt expansion (and inflation). 

Lift off in a world of excess reserves

Back in the good ol' days, U.S. depository institutions (mostly banks) held just enough cash reserves (deposits they held at the Fed) to meet their settlement needs. At the end of the day, a bank short of reserves could borrow them from a bank with excess reserves. These trades would occur on the so-called federal funds market and the interest rate agreed upon on these (unsecured) overnight loans is called the federal funds rate (FFR). In fact, there was (and is) no such thing as "the" FFR because these trades did not (and do not) occur in a centralized market at a single price. Trades in the FF market occur in decentralized over-the-counter markets, with the terms of trade (interest rates) varying widely across transactions (see figure 12 here). "The" FFR we see reported is sometimes called the effective FFR. The effective FFR is just a weighted average of reported interest rates negotiated in the federal funds market.

For better or worse, the FFR was (and still remains) the Fed's target interest rate. Prior to 2008, the Fed (actually, the FOMC) would choose a FFR target rate and then instruct the open markets trading desk at the New York Fed to engage in open market operations (purchases and sales of short-term Treasury debt) to hit the target. To raise the FFR, the trading desk would sell bonds, to lower it, they would buy bonds. (Evidently, even the mere "threat" of buying and selling bonds following an FOMC policy rate announcement often seemed sufficient to move the market FFR close to target.) The way this worked was as follows. A sale of bonds would drain reserves from the banking system, compelling banks short of cash in the FFR market to bid up the FFR rate. A purchase of bonds would induce the opposite effect. The system worked because banks were compelled to economize as much as they prudently could on their reserve balances. Prior to 2008, the Fed was legally prohibited from paying interest on reserves (IOR).

But the world is now changed. In 2008, the Fed started paying a positive IOR (25 basis points). And it started buying large quantities of U.S. treasury and agency debt. The Fed funded these purchases with interest-bearing reserves. It may seem like a strange thing to do, but from a banker's perspective it looks brilliant. Imagine buying a risk-free asset yielding 2-3% and funding the purchase by borrowing at 1/4%. The profit the Fed makes on this spread is mostly remitted to the U.S. treasury (i.e., the taxpayer). In 2014, the Fed remitted close to $100B.

The U.S. banking system is now flush with reserves--most depository institutions (DIs) hold "excess" reserves. (Incidentally, there is no way for the banking system collectively to "get rid" of these excess reserves. In particular, the banking system as a whole cannot "lend out reserves.") And since most DIs have excess reserves, the FFR market is essentially dead.

Well, not quite dead. There are still a few trades, motivated  primarily by the fact that some key participants in the FF market (GSEs) are legally prohibited from earning IOR. The Federal Home Loan Banks, in particular, have a large supply of funds that, if they could, would happily hold these deposits at the Fed earning 25bp. Instead, they must hold these funds with DIs, who are able to earn IOR (see here). Because short-term treasury debt is yielding close to zero, the effective FFR negotiated between DIs and non-DIs lies somewhere between zero and IOR (see following graph). According to Afonso and Lagos (2014),  the volume of trade in the FF market has dropped to about $40B per day from its peak of $150B per day prior to 2008 (see their figure 4).

Alright, so where are we at? Since 2008, the Fed has congressional authority to pay IOR (to DIs only). The Fed can clearly set IOR where ever it wants (within limits). So when lift off date arrives, raising IOR by (say) 25bp will pose no problem from an operational viewpoint.

The Fed, however, has elected to keep the FFR--not the IOR--as "the" policy rate. Given this choice, there is the question of how the Fed expects to influence the FFR when there is no (or very little) FF market left in this world of excess reserves. Theoretically, IOR should serve as a floor for the FFR. But evidently there are "balance sheet costs" and other frictions that prevent arbitrage from working its magic. So the problem (for the Fed) is how to guarantee that its policy rate--the FFR--will lift off along with an increase in IOR.

Enter the Fed's new policy tool -- the overnight reverse repo (ON RRP) facility, overseen by Simon Potter of the NY Fed. Actually, the tool is not exactly new. The Fed has historically used repos and reverse repos for a long time; see the following graph.

In a repo exchange, the Fed buys (borrows) a security from a DI in exchange for reserves. In this case, the DI is borrowing reserves from the Fed. The value of the Fed's repo holdings is plotted in red above. Since the advent of QE, the repo facility has remained dormant. In a reverse repo, the Fed sells (lends) a security to a DI in exchange for reserves. In this case, the DI is lending reserves to the Fed--that is, reverse repo is just a way for the Fed to pay interest on reserves. The blue line above plots the value of reverse repo holdings.

What's new about the ON RRP facility is that it is open to an expanded set of counterparties (beyond the regular set of DIs). The NY Fed publishes a list of these counterparties here. It is notable that GSEs and MMMFs are including in this list.

Lift-off (an announced increase in the FFR target rate or band) will then be accompanied by an increase in the IOR to (say) 50bp together with an ON RRP rate of (say) 25bp. The hope is for the effective FFR to trade somewhere within this interest rate band. Theoretically, the ON RRP rate should provide an effective floor for the FFR--assuming that the facility is conducted on a full allotment basis (i.e., assuming that the facility is not capped in some manner). If the facility is capped, and if the cap binds, then we may observe trades in the FF market occurring at rates lower than the ON RRP rate. This latter scenario is obviously one that the Fed would like to avoid.

There is also the question of whether other market interest rates will follow the FFR upward in the present environment. Some economists, like Manmohan Singh of the IMF worry that the Fed is using the wrong tool for lift off (see his piece in the Financial Times here). Singh would prefer outright asset sales because the treasuries released in the market can then be left to circulate (via re-use and rehypothecation) to relieve an ongoing asset shortage. (The securities released by the Fed in its ON RRP facility are evidently not expected to circulate.) It is conceivable, though perhaps unlikely, that the yield on short-term treasuries remains close to zero (reflecting a stubborn liquidity premium) even as the FFR is increased. As always, it will be interesting to see what actually transpires.

Bitcoin and central banking

Economic exchange depends critically on secure and trustworthy payment systems. Because payment systems are fundamentally about recording and communicating information, it should come as no surprise that payment systems have evolved in tandem with advancements in electronic data storage and communications. One exciting development of late is Bitcoin--an algorithmic-based, communally-operated money and payment system. I thought I'd take some time to gather my thoughts on Bitcoin and to ponder how central banks might respond to this innovation.

Bitcoin is open-source software designed to govern a money and payment system without the aid of conventional intermediaries like chartered and central banks. The role of chartered banks as payment processors is replaced by a communal consensus protocol (mining), where transaction histories are recorded on an open ledger (the blockchain). The role of a central bank is replaced by a "fixed" money supply rule (Note: nothing is truly "fixed" in Bitcoin since the community could, in principle, "vote" to change program parameters at subsequent dates. This is true, of course, for any system of governance.)
   
Bitcoin is about as close as we have come to digital cash. And because the bitcoin is in relatively fixed supply (or so we think), people sometimes refer to Bitcoin as managing a digital-gold system.

Let's think about cash for a minute.  Cash is a bearer instrument (ownership is equated with possession). Cash payments are made in a P2P manner, without the aid of an intermediary. When I buy my morning coffee, I debit my wallet of cash and the merchant credits her register by the same amount. There is a finality to the transaction (unless my coffee is cold and the merchant values my future business). To the extent that cash is difficult to counterfeit, it solves the double-spend problem. The use of a cash-based payment system is "permissionless" (no application process is needed to open a cash wallet, no personal information needs to be relinquished to open an account). Relatedly, cash is "censorship-resistant," meaning that you can basically spend it as you see fit. Finally, cash is distributed on an invisible ledger, permitting a degree of anonymity. Cash transactions need not leave a paper trail.
     
The digital money issued by banks is different from cash in several respects. One main difference is that transactions between any two traders must be intermediated by a bank. Transactors implicitly trust the bank to do the proper book-keeping and it is this trust that "solves" the double-spend problem for digital bank money. Bank money is not permissionless. One has to make an application for a bank account and, in the process, relinquish a great deal of personal information that one trusts the bank to keep secure. People who are unable to properly identity themselves are denied conventional banking services (up to 1/4 of American households are estimated to be unbanked or underbanked). Bank money is not censorship resistant--banks may not process certain types of payment requests on your behalf. Of course, bank money leaves a digital trail (albeit on a system of closed ledgers) with your identity clearly attached to a particular transaction history.

So what are the benefits of Bitcoin? The benefits are likely to vary from person to person, but in general, I'd say the following. First, it's monetary policy reduces the "hot potato" motive of economizing on money balances--that is, it offers the prospect of being a decent long-run store of value. Second, anyone with access to the internet can access an account (a public/private key pair) for free--like cash, no permission is needed. The public key is like an account number and the private key is like a password. Account balances remain secure as long as the private key remains secure. Third, like cash, no personal information is necessary to open an account, so no need to worry about securing private information. Fourth, like cash, bitcoin is censorship resistant--no one can prevent you from spending/receiving bitcoin from whomever you like. Fifth, bitcoin can offer a greater degree of anonymity than bank deposit money, but less so than cash (unlike cash, the blockchain ledger is visible and public). Sixth, the entire money supply (blockchain) lives on a replicated distributed ledger--it lives simultaneously everywhere--so that "sending money somewhere" means updating the ledger on all computers everywhere. There are no banks, there are no borders. Seventh, the user cost of transferring value is relatively low.

As I said, the extent to which consumers value these benefits likely depends on a host of factors. I see potentially large benefits to relatively poor individuals who have limited access to conventional banking services. It is estimated that up to one in four U.S. households are unbanked or underbanked--people who must rely on high-cost bill-pay, prepaid debit cards, check cashing services, and payday loans. The benefits are likely to be greater for poor individuals living in high inflation regimes that do not have access to interest-bearing (inflation protected) accounts.

What are the costs of Bitcoin? First, it is not a unit of account. Because of its monetary policy and its unstable demand, its value is quite volatile over short periods of time, making it inconvenient as a payment instrument (even if it is a good long-run store of value). Second, it has the same security properties as cash--losing or forgetting your private key is like losing your wallet. One could employ the services of a third-party in this regard, but if so, then why not just use a bank? Third, although the user cost of Bitcoin is presently low, the social cost (primarily in the form of electricity) is high relative to the cost of operating trusted ledgers. Fourth, because of its cash-like properties, bitcoin can also help facilitate illicit trade. (Of course, the same is true of cash.)

How might the advent of Bitcoin influence central bank thinking?

First, the threat of Bitcoin (and of currency substitutes in general) places constraints on monetary policy. In jurisdictions that finance large amounts government spending through the inflation tax, such a constraint may become binding.

Second, to the extent that bitcoin becomes a significant payment instrument (or even the unit of account), it might open the door to financial instability. Experience demonstrates the private sector's desire for maturity transformation or, more generally, the willingness to act on incentives that make funding illiquid assets with short-term debt a preferred balance sheet structure. The same incentives would presumably be in place in a Bitcoin economy. In principle, demand-like liabilities should trade at a risk premium. But in practice, they may not. Especially in times of economic complacency, they are likely to be viewed as close to perfect substitutes in terms of their money properties, just like bank money and cash today (and the way U.S. treasury debt and senior tranches of private-label MBS were viewed as close collateral substitutes in the repo market prior to 2008). The question is what happens if and when there is a "bank-run" or "roll-over crisis" on such a system? The situation is exacerbated if bitcoin is not the unit of account (think of European banks issuing loans denominated in USD). Since federal deposit insurance may not be available and since no LOLR can issue BTC, a classic bank panic is possible. Central banks and fiscal authorities would have to think about what, if anything, to do in such circumstances. One solution may be to impose narrow banking restrictions for banks (and other entities) engaged in bitcoin-denominated maturity transformation.

My own recommendation is for central banks to consider offering digital money services (possibly even a cryptocurrency) at the retail and wholesale level. There is no reason why, in principle, a central bank could not offer online accounts, the same way the U.S. Treasury presently does (www.treasurydirect.gov). These accounts would obviously not have to be insured. They would provide firms with a safe place to manage their cash without resorting to the banking or shadow banking sector. They would give monetary policy an additional instrument--the ability to pay interest on low-denomination money (possibly at a negative rate). To the extent paper money is displaced, there would be large cost savings as well.

It's hard (for me) to see what the downsides are in having a central bank supply digital money. Critics might argue that it leaves people exposed to potentially poor monetary policy. This may be true and, for these people, currency substitutes should be available (including Bitcoin). In terms of payments, critics might argue that central bank accounts will be permissioned accounts, requiring the release of personal information, application efforts, that KYC restrictions will apply (so not censorship resistant) and so on. To address these concerns, a central bank could go one step further and issue a cryptocurrency (Fedcoin) offered at a fixed exchange rate where payments are cleared using a Bitcoin-inspired anonymous communal consensus algorithm. I don't think we can expect anything like this in the near future, but it is technologically possible. Of course, people will complain that Fedcoin will inspire illicit trade, etc. But again, the same is true of regular central bank issued cash.

There is the question of how such an innovation might impact traditional banking models. I'll leave this question for another post. 

Fisher without Euler

The Neo-Fisherian proposition is that raising the nominal interest rate (and keeping it elevated) will eventually cause inflation to rise (see Steve Williamson's explanation here.)

The basic idea revolves around the so-called Fisher equation:

R = r + E[p]

where R is the nominal interest rate, r is the real interest rate, and E[p] is the expected rate of inflation. If bond buyers expect inflation to increase then they'll ask for more compensation in the form of a higher nominal interest rate (a lower bond price).

The conventional idea is that monetary and fiscal policies (in particular, the expectation of how these policies will unfold over time) largely determined inflation expectations E[p]. In conventional (modern) macro economic theories, expectations are assumed to be formed "rationally" (i.e., in a manner that is consistent with the stochastic processes that actually govern the economy).

Neo-Fisherians reverse this conventional direction of causality. They argue that increasing R leads people to revise their inflation expectations upward. And because people have rational expectations, for these expectations to be consistent with reality, actual inflation will (somehow) have to increase.

As far as I can tell, this Neo-Fisherian proposition comes in two stripes. The first stripe is of the "cashless economy with Ricardian equivalence" variety--the models that Michael Woodford likes to use. In this class of models, "balance sheets don't matter." And because central bank money and government bonds are just ways of labeling the liabilities of the consolidated government sector, they don't matter for determining (among other things) the price-level. In this class of models, inflation expectations are somehow assumed to adjust to satisfy the Fisher equation. And then the price-setting behavior of firms (who set prices in an abstract unit of account but do not actually accept payment in any monetary object) adjusts in a manner that is consistent with higher expected inflations. Personally, I find this view implausible. Moreover, it's frustrating that no one promoting this view seems willing or able to explain how/why all this is supposed to happen (beyond repeating the phrase "the Fisher equation must hold" or "it's a rational expectations equilibrium").

The second stripe of this proposition, however, seems more plausible (at least, in principle) to me. In this world, balance sheets matter. The supply and composition of the government's assets and liabilities matter. And in particular, the time-path of the total nominal government debt (and its composition) matters for determining the price-level. The idea here is that when the central bank announces a higher R, there is a corresponding passive accommodation of central bank policy on the part of the fiscal policy to increase the rate of growth of total government debt (i.e., cut taxes, or engage in "helicopter drops"). If the fiscal authority behaves "passively" in this sense, then people will rationally expect higher inflation--and the higher inflation will actually transpire not because people expected it, but because the fiscal authority delivered it. I think this is an interpretation that even Nick Rowe agrees with (see here).

Both versions of the Neo-Fisherian proposition above seem to rely heavily on the notion of rational expectations. In my previous post, I speculated that the proposition might hold even if people had non-rational "adaptive" expectations. The idea I had there was that if a sudden increase in R caused to the price-level to jump up (instead of down, which is the usual presumption), then people with adaptive expectations will revise their inflation expectations upward (not downward).  An initial increase in the price-level might happen if, for example, the higher interest rate led to higher operating expenditures on the part of firms. Following this initial impulse, the actual path of inflation would be determined either by (stripe 1) the nature of learning dynamics or (stripe 2) the manner in which policy accommodates itself to the price shock (e.g., see Christiano and Gust, 1999).

In response to my post, Erzo Luttmer alerted me to his paper Fisher without Euler, in which he claims that the Neo-Fisherian proposition pops out of a model in which people are not forward-looking at all. The argument, as far as I can tell, relies heavily on how the government debt-service cost is financed. Let me try to explain (you can refer to Erzo's paper and short note to see whether I have it right).

Let's start with the government budget constraint,

G(t) - T(t) = q*B(t) - B(t-1)

where T(t) denotes tax revenue, G(t) government purchases, and B(t-1) denotes bonds maturing to cash at date t. Let 0 < q < 1 denote the price of a bond (1/q is the gross nominal interest rate, set by the Fed). For simplicity, I think we can set G(t) = 0 for all t, so that

T(t) = B(t-1) - q*B(t)

This makes it clear how a lower q (higher interest rate) means either  higher taxes and/or higher debt level. Now, let p(t) denote the price-level and define τ = T(t)/p(t). Assume that nominal debt grows at a constant rate, B(t) = μB(t-1). Now use this notation to rewrite the government budget constraint above as

τ = (1 - q*μ)*B(t-1)/p(t)

To close the model, we need a theory of the price-level. The simplest theory I can think of is the Quantity Theory: p(t) = B(t-1)/y(t), where y(t) is real income (and velocity is held constant), so that B(t-1)/p(t) = y(t). If we treat y(t) as exogenous, then it follows immediately that lowering the interest rate (increasing q) necessitates a decline in inflation (μ). So lowering the interest rate lowers the debt-service cost of debt which (for given real spending and taxation levels) means that the supply of nominal debt need not grow as quickly -- as the growth rate in the supply of "money" declines, so does inflation. The Neo-Fisherian result follows even without forward-looking behavior.

Erzo does not use the simple version of the Quantity Theory as I did here. Instead, he assumes that individuals adopt a simple behavioral rule (consumption function):

c(t) = α(y(t) - τ) + βB(t-1)/p(t)

where α is the propensity to consume out of disposable income and β is the propensity to consume out of wealth (here in the form of real bond holdings). If we let g(t) denote real government purchases, then goods-market-clearing requires:

c(t) = y(t) - g(t)

Erzo then combines these latter two equations to determine the price-level p(t), treating y(t) and g(t) as exogenous (as did I).

At the end of the day, it's a simple point. Still, I think it's an important one to keep in mind since I am reading in more than one place that the Neo-Fisherian proposition depends on rational expectations. Evidently, it does not.

NeoFisherism without rational expectations

Is the Fed's "zero-interest-rate policy" (ZIRP) inflationary or deflationary? You'd think that macroeconomists would have a straight answer for such a simple question. But we don't. As usual, the answer seems to depend on things.

Someone once joked that an economist is someone who sees something work in practice and then asks whether it might work in theory. Well, appealing to the evidence is not much help here either. We have examples like that of Volcker temporarily raising rates (by lowering the money supply growth rate) to lower inflation in the early 1980s. But then we have the present counterexample of ZIRP, which seems to be having little effect in raising inflation. Indeed, the Fed has consistently missed its 2% inflation target from below for years now (see Understanding Lowflation).

Some economists suggest that there are theoretical reasons to support the notion that ZIRP is deflationary. The proposition that targeting a nominal interest rate at a low (high) level results in low (high) inflation is known as "NeoFisherism." The idea goes back at least to Benhabib, Schmitt-Grohe and Uribe (2001) in their The Perils of Taylor Rules. The idea has been taken seriously in policy circles. My boss, St. Louis Fed president Jim Bullard wrote about it here in 2010. You can read all about the recent controversy here: Understanding the NeoFisherite Rebellion.

The basic idea behind NeoFisherism is the Fisher equation:

FE1: Nominal interest rate = real interest rate + expected inflation.

One interpretation of the Fisher equation is that it is a no-arbitrage-condition that equates the real rate of return on a nominal bond with the real rate of return on a real (e.g., TIPS) bond. FE1 implicitly assumes that the risk and liquidity characteristics of the nominal and real bond are identical. Steve Williamson and I consider a model where the nominal bond (potentially) carries a liquidity premium, in which case FE1 becomes:

FE2: Nominal interest rate + liquidity premium = real interest rate + expected inflation.

I'm not aware of any economist that disputes the logic underlying (some version of) the Fisher equation. The controversy lies elsewhere. But before going there, let me describe the way things are supposed to work in neoclassical theory.

Start in a steady-state equilibrium where FE1 holds. Now consider a surprise permanent increase in the nominal interest rate. What happens? Well, a higher nominal interest rate increases the opportunity cost of holding money, so people want to economize on their money balances. However, because someone must hold the outstanding stock of money, a "hot potato effect" implies that the equilibrium inflation rate must rise (the real rate of return on money must fall). In the new steady-state equilibrium, real money balances are lower (the price-level and the inflation rate are higher than they would have been prior to the policy shock). If people have rational expectations, then absent any friction, inflation expectations jump up along with actual inflation. If there are nominal rigidities, then inflation may (or may not) decline for a while following the shock, but in the long-run, higher interest rate policy leads to higher inflation. [Aside: my own view is that a supporting fiscal policy is needed for this result to transpire; see here: A Dirty Little Secret.]

The conventional wisdom, however, is that pegging the nominal interest rate is unstable. Suppose we begin, by some fluke, in a steady-state where FE1 holds. Now consider the same experiment but assume that people form their expectations of inflation through some adaptive process; see Howitt (1992). For example, suppose that today's inflation expectation is simply yesterday's inflation rate. Then an increase in the nominal rate must, by FE1, lead to an increase in the real interest rate. An increase in the real interest rate depresses aggregate demand today (consumer and investment goods). The surprise drop in demand leads to a surprise decline in the price-level--the inflation rate turns out to be lower than expected. Going forward, people adapt their inflation forecasts downward. But given FE1, this implies yet another increase in the real interest rate. And so on. A deflationary spiral ensues.

For those interested, refer to this more detailed discussion by John Cochrane: The Neo-Fisherian Question.

Now, the thought occurred to me: what if we replace the assumption of rational expectations in my model with Williamson (cited above) with a form of adaptive expectations? What would happen if we performed the same experiment but, beginning in a steady-state where there is an "asset shortage" so that the FE2 version of the Fisher equation holds. My back-of-the-envelope calculations suggest the following.

First, because expected inflation is fixed in the period the nominal interest rate is raised, FE2 suggests that either the real interest rate rises, or the liquidity premium falls, or both. In our model, there is substitution out of the cash good into the credit good. But because there is a cash-in-advance constraint on the cash good, i.e., p(t)c(t) = M(t), it follows that a decline in the demand for c(t) corresponds to a decline in the demand for real money balances--that is, the price-level p(t) must jump up unexpectedly (for a given money supply M(t)).

Now, given the surprise jump in the price-level, an adaptive expectations rule will adjust the expected rate of inflation upward. What happens next depends critically on the properties of the assumed learning rule, the policy rule, etc. For my purpose here, I make the following assumptions. Suppose that the economy remains in the "asset shortage" scenario and assume that the government fixes the money growth rate at exactly the new, higher, adaptively-formed, inflation expectation. In this case, the economy reaches a new steady-state with a higher interest rate, an arbitrarily higher inflation rate, and an arbitrarily lower liquidity premium (conditional on the liquidity premium remaining strictly positive). [Note: by arbitrary what I mean is that the new inflation rate is determined, under my maintained assumptions, by the initial surprise increase in inflation, which may lie anywhere within a range such that the liquidity premium remains positive. In the absence of a liquidity premium, the inflation rate would rise one-for-one with the nominal interest rate.]

I hope I made my point clear enough. The claim that increasing the nominal interest rate leads to higher inflation does not depend on rational expectations as is commonly claimed. A simple adaptive rule could lead to higher inflation expectations. The key is whether the price-level impact of increasing the nominal interest rate is positive or negative. If it's positive, then people will revise their adaptive expectations upward and, depending on the learning rule and policy reaction, the ensuing inflation dynamic could play itself out in the form of permanently higher inflation. The NeoFisherite proposition is possible even if people do not have rational expectations.

Postscript Nov. 01, 2015
Tony Yates suggests the cost channel in Ravenna and Walsh (2006)  together with least-squares learning might deliver the same result. It's a good idea. Somebody should try to work it out! 

Zero intolerance

In an earlier post, I summarized the main arguments people have used for and against a September lift-off.  There are, of course, other arguments one can make and bond guru Bill Gross isn't shy about offering his view on the matter in his September 23 2015 investment outlook.

According to Gross, the Fed's low interest rate policy constitutes a form of "financial repression." His argument, as far as I can tell, goes as follows. Long-term prosperity depends on the stock of productive capital. The stock of productive capital is augmented by investment (the flow of newly produced capital goods). Investment is financed out of saving. Low interest rates discourage saving. Therefore, low interest rates are ultimately a prescription for secular stagnation.

Gross claims that "no model will lead to this conclusion." I'm not exactly sure what he means by that. I think what he means "forget about theory, let's just look at the facts." Unfortunately, facts do not always speak for themselves.

So what sort of evidence does he select to support his conclusion? He begins by noting that inflation-adjusted interest rates (on high-grade bond instruments, I presume) were on average negative over the period 1930-1979 and on average positive since then (thanks to Volcker) until recently. Here's what the data looks like since the end of the Korean war (FRED only gives me the interest rate series since then).

The blue line plots the nominal yield on a one-year treasury, the red line plots the one-year CPI inflation rate. Blue minus red gives us a measure of the realized inflation-adjusted return on a nominally risk-free security. Returns were relatively high in the 1960s, 1980s, 1990s, and relatively low in the 1970s, 2000s, and 2010s (so far).

In relation to this observation, Gross writes approvingly of Fed policy decisions in the early 1980s:

But then Paul Volcker turned the bond market upside down and ever since (until 2009), financial markets enjoyed positive real yields and a kick in the pants boost to other asset prices, as those yields gradually came down and increased the present value of bonds, stocks and real estate.

This is a bizarre statement in some respects. First, as the data above makes clear, it was nominal yields that gradually came down--real yields remained elevated for two decades after the event. Second, he evidently does have a model of how a policy-induced increase in the nominal interest rate leads to prosperity: as yields march downward from an elevated level, capital gains are realized in a broad range of asset classes. This is a bizarre argument both in its own right and because it ignores the initial capital losses realized on wealth portfolios when the policy rate is suddenly increased.

So, no, I don't think that model makes much sense. But if so, then how do we make sense of the data? The fact is that the U.S. economy generally did prosper after the 1981-82 recession. Most economists attribute this subsequent era of prosperity in part to the fact that Volcker's policies ushered in an era of low and stable inflation. Jacking up the interest rate was just a temporary measure to bring inflation down. And once inflation began to drift down, nominal yields declined because of the Fisher effect. The fact that real yields remained elevated was just the by-product of an accelerated growth in productivity (after the 1970s productivity slowdown) that likely had little to do with monetary policy.

But maybe this conventional interpretation is incorrect. Could Gross be on to something? Maybe there is a model that justifies his conclusion. I've been thinking about this lately, wondering just what such a model would look like. Here is what I came up with.

Consider a textbook macro model. Let S(r,y) denote the supply of saving, assumed to be increasing in real income y (GDP) and the real interest rate r. Let I(r,x) denote the demand for investment, assumed to decreasing in the real interest rate r and increasing in the expected productivity of capital investment, x.

In a closed economy, domestic saving must equal domestic investment, so S(r,y) = I(r,x). This equation gives us the famous IS curve: the locus of (y,r) combinations consistent with S=I. This relation exists, in one form or another, in virtually every macro model I'm aware of.

The neoclassical view is that the market, left to its own devices, will determine a "full employment" level of income, y*. With y* so determined, the equilibrium rate of interest r* is determined by market-clearing in the loanable fund market, S(r*,y*) = I(r*,x).

Business cycles are generated by fluctuations in the x. High x is associated with optimism, low x with pessimism (over the expected return to capital spending). The diagram below demonstrates what happens when the economy switches from an optimistic outlook to a pessimistic outlook. Let point A denote the initial equilibrium position. A decline in x to x' shifts the investment demand schedule downward. Lower investment demand puts downward pressure on the interest rate--the economy moves along the saving schedule from point A to B. If depressed expectations persist, then the lower level of investment leads to a lower stock of productive capital. This has the effect of depressing GDP. As income declines from y* to y', the saving schedule shifts down and the economy moves from point B to C.

Point C is characterized by lower income, lower investment, lower saving and a lower real interest rate. This is the neoclassical explanation for why periods of why real interest rates are procyclical. Low interest rates are not the product of "financial repression." They are symptomatic of a depressed economic outlook. And any attempt to artificially increase the real interest rate is going to make things worse, not better. One cannot legislate prosperity by increasing the interest rate.

Now, if I understand Gross correctly, he seems to be saying that present circumstances are not the byproduct of depressed expectations. The problem is that the Fed is keeping the real interest rate artificially low. Let's try to interpret this view in terms of the following diagram. The economy naturally wants to be at point A, where the interest rate is higher, along with saving, investment and income. But the Fed is keeping the interest rate artificially low--at zero, in the diagram below.

The effect of the zero interest rate policy is to discourage saving. While the demand for investment is high (point D), there's not enough saving to finance it (point B). As such, the level of investment falls from A to B. The lower investment eventually translates into lower GDP. As income declines, the saving schedule shifts down and the economy eventually settles at point C. This is secular stagnation brought about by the Fed's financial repression.

So is this a sensible argument? There is a problem with it that Gross touches on in his piece when explaining how low interest rates are harmful:

How so? Because zero bound interest rates destroy the savings function of capitalism, which is a necessary and in fact synchronous component of investment. Why that is true is not immediately apparent. If companies can borrow close to zero, why wouldn’t they invest the proceeds in the real economy? The evidence of recent years is that they have not.

Indeed, the logic of the argument is not apparent at all. With interest rates so low, the business sector should be screaming for funds to finance huge new capital expenditures (point D in the diagram above). But they are not. Why not? At this stage, he simply abandons the logic and refers to the evidence. As if the evidence alone somehow supports his illogical argument.

There are, in fact, some logical arguments that one can use to interpret the facts. One is given by the neoclassical interpretation in the first diagram above. Expectations are depressed because the investment climate is poor (feel free to make a list of reasons for why this is the case). The demand for investment is low. Low investment demand is keeping the real interest rate low. The Fed is just delivering what the market "wants" in present circumstances. Raising the interest rate in the present climate would be counterproductive.

There is another argument one could make. Suppose that the investment climate is not depressed. There are loads of positive NPV projects out there just waiting to be financed. Unfortunately, financial conditions are such that many firms find it difficult to find low-cost financing to fund potentially profitable investment projects. In the wake of the financial crisis, creditors still do not fully trust debtors to make good on their promises. As well, regulatory reforms like the Dodd-Frank Act may make it more difficult to supply credit to worthy ventures. In the lingo used by macroeconomists, firms may be debt-constrained. The situation here is depicted in the following diagram.

The debt-constraints that afflict the business sector's investment plans caps the total amount of investment that will be financed by creditors--the investment demand schedule effectively becomes flat at this capped amount. The financial crisis moved the economy from point A to B. As before, lower investment ultimately reduces the productive capacity of the economy, so that income declines. The decline in income shifts the saving schedule down--the economy moves from B to C. The equilibrium interest rate is low--not because of Fed policy, but because investment is constrained. Savers would love to extend more credit if investors could be trusted and if regulatory hurdles were removed. But alas, present circumstances do not permit this saving flow to be released (except, potentially, to finance government expenditures or tax cuts). The effect of a policy-induced increase in the interest rate in this case would be to lower income even further. (The saving schedule would have to shift down even further to ensure that S=I.)

If the analysis above is correct, then the recommendation to increase interest rates in the present climate is off base. Low interest rates are not the cause of our ills--they are symptomatic of deeper problems. The way to get interest rates higher is to adopt policies that would stimulate investment demand (the neoclassical view) and/or adopt measures that would remove financial market frictions (the debt-constraint view). A deficit-financed tax cut (or subsidy) on investment spending would constitute one such measure.

There are, of course, other models that one could use to justify a policy-induced increase in the interest rate in present circumstances. Some members of the FOMC, for example, view the economy as having largely recovered and are now worried about the effect of very low interest rates on the prospect of future inflation. These types of arguments, however, are quite a bit different from the Gross hypothesis. But if he wants higher interest rates, maybe he should use them! A bit of a warning though: I don't think his bond portfolio is going to like the consequences.

The costs of interest rate liftoff for homeowners

The results of some interesting experiments to report here from the work of my colleague Carlos Garriga and his coauthors, Roman Sustek and Finn Kydland. DA

The statement from the July meeting of the Federal Open Market Committee reveals a support for starting to increase interest rates this Fall, provided some further improvement in the labor market. Such monetary policy stance is currently held also by policy makers in the U.K., as hinted by some members of the Monetary Policy Committee, the rate-setting body of the Bank of England.

An important channel through which interest rates affect the typical household is the cost of servicing mortgage debt. Standard mortgage loans require homeowners to make nominal installments—regular interest and amortization payments—calculated so that the loan is fully repaid by the end of its term. Changes in the interest rate set by the central bank affect the size of these payments, but differently for different types of mortgage loans. In addition, the real value of these payments depends on inflation.

Mortgage contracts and debt servicing costs

Fixed-rate mortgages (FRM), characteristic for the U.S., have a fixed nominal interest rate and thus constant nominal installments for the entire term of the loan, typically 15 or 30 years. The FRM interest rate is determined at origination on the basis of the mortgage lenders’ expectations of the future path of the central bank interest rate. In contrast, the interest rate of adjustable-rate mortgages (ARM), a standard contract in the U.K., changes every time the central bank interest rate changes. The nominal installments of ARM loans are thus recalculated on every such occasion, to ensure the full repayment of the loan by the end of its term.[2]

While mortgage contracts specify nominal installments, either fixed of adjustable, the real cost of servicing mortgage debt depends on inflation. The effects of the liftoff on homeowners will therefore depend not only on the mortgage type and the future path of interest rates but also on what happens to inflation during the liftoff.

It is instructive to illustrate the effects of the liftoff on homeowners in terms of changes in mortgage debt servicing costs (DSC)—nominal mortgage payments deflated by inflation as a fraction of household real income. This variable provides a metric of the burden of mortgage debt to homeowners as it measures the fraction of real income homeowners have to give up to meet the mortgage payment obligations of their contract. The numerical examples below illustrate these points.[3]

Liftoff scenarios

Figure 1 considers two alternative paths of the central bank interest rate, a slow liftoff and a fast liftoff from the current nearly zero lower bound (ZLB). In both cases, the interest rate is assumed to revert to 4 percent, the pre-2007 crisis average. In the fast liftoff case, it reaches the half-way mark of 2 percent in two years’ time, whereas in the slow liftoff case this mark is not reached until about eight years from the start of the liftoff. 

Figure 2 plots DSC in the case of liftoff that is not accompanied by an increase in inflation. In this case the path of the nominal interest rate in Figure 1 coincides with the path of the real interest rate. Figure 3 contrasts this case with a situation where the increase in the central bank interest rate is accompanied by a one-for-one increase in the inflation rate. In this case, the real rate is left unchanged at zero percent and the path of the nominal interest rate in Figure 1 is equivalent to a path of the inflation rate. While both assumptions are extreme, they demonstrate how the effects of the liftoff depend on the inflation rate.

In both figures, the DSC under the various liftoff scenarios are compared with a baseline case, in which both the central bank interest rate and the inflation rate stay unchanged at zero percent (blue dotted line), approximately the current situation. In this case, DSC are about 20 percent due to the assumed lenders’ markup of three percentage points.

A liftoff without inflation

When inflation stays at zero percent during the liftoff (Figure 2) the real mortgage payments of existing homeowners with FRM loans are unaffected. This is because the FRM interest rate has been fixed at origination before the liftoff and inflation stays at zero percent. However, new FRM loans will be priced according to the expected path of the central bank interest rate in Figure 1 and will therefore carry a higher interest rate. The new FRM interest rate is higher the faster is the liftoff. In the case of the fast liftoff, the higher interest rate implies DSC of almost 30 percent; under the slow liftoff, DSC will be 25 percent (the solid red lines in Figure 2).

When mortgages are ARM, the liftoff affects both, existing and new homeowners. The dashed green lines plot DSC for new ARM homeowners and essentially track the paths of the central bank interest rate—DSC gradually increase from 20 percent to 32 percent under the fast liftoff and to 27.5 percent under the slow liftoff. For existing homeowners with ARM the effects depend on when the loan was originated. The more recently originated was the loan the more will the path of DSC resemble that for new loans. DSC of loans that are almost repaid will be almost immune to the liftoff. This is not only because the debt outstanding gets smaller over the life of the loan, but also because mortgage payments in later periods of the life of the loan are mostly amortization payments, rather than interest payments.

A liftoff accompanied by inflation

When the liftoff is accompanied by equivalent increase in inflation, and no change in the real rate, the impact of the liftoff on DSC is greatly attenuated (Figure 3). First, existing FRM homeowners gain from the higher inflation and these gains grow over time as persistent inflation deflates the real value of the nominal payments, which under FRM are constant. Those with the more recently originated mortgages gain the most over their homeownership tenure (the dash-dotted red lines in the figure show the case of a mortgage with 119 quarters remaining; that is 29 years and 3 quarters). New FRM borrowers, however, will face a higher mortgage rate and, as a result, initial DSC of almost 30 percent in the fast liftoff case (solid red line). But the real value of those payments will also gradually decline over time.  

For ARM homeowners, both the existing and new homeowners, there are two opposing forces in place. On one hand, higher nominal interest rates increase nominal mortgage payments. On the other hand, higher inflation reduces their real value. The first effect is stronger initially but the second effect dominates over time. Furthermore, the point where the second effect starts to bite depends on the speed of the liftoff. While in the fast liftoff case the first effect dominates for the first eight years (32 quarters), in the slow liftoff case it hardly bites at all (dashed green lines).

Policy implications

To sum up, the effects of the liftoff on homeowners depend on three factors: (i) the prevalent mortgage type in an economy (FRM vs ARM), (ii) the speed of the liftoff, and (iii) what happens to inflation during the course of the liftoff.

If inflation stays constant at near zero then in the U.S., where FRM loans dominate, the liftoff will affect only new homeowners. In the U.K., where ARM loans dominate, the negative effects will in contrast be felt strongly by both new and existing homeowners.

However, if the liftoff is accompanied by sufficiently high inflation as in our examples, the negative effects will be much weaker in both countries. In the U.S., the initial negative effect on new homeowners will be compensated by positive effects on existing homeowners. And in the U.K., provided the liftoff is sufficiently gradual, neither existing nor new homeowners may face significantly higher real costs of servicing their mortgage debt.

Therefore, if the purpose of the liftoff is to “normalize” nominal interest rates without derailing the recovery, central bankers in both countries should wait until the economies convincingly show signs of inflation taking off. Furthermore, the liftoff should be gradual and in line with inflation.

Buzz words: “If the purpose of the liftoff is to “normalize” nominal interest rates without derailing the recovery, the Federal Reserve Bank and the Bank of England should wait until the economies show convincingly signs of inflation taking off.”

Carlos Garriga

Research Officer

Federal Reserve Bank of St. Louis

(314) 444-7412

carlos.garriga@stls.frb.org

---

[2] In the U.K., the typical mortgage is the so-called standard-variable rate mortgage, which has an interest rate fixed for the first year or two. After this initial period, the interest rate can vary at the discretion of the lender, but usually the resets coincide with changes in the Bank Rate, the Bank of England policy interest rate. A “tracker” mortgage is explicitly linked to the Bank Rate. Here we abstract from these details.

[3] The examples assume that a homeowner’s real income does not change throughout the life of the loan, the loan at origination is four times the homeowner’s income, and mortgage lenders’ mark-up over market interest rates is three percentage points.r market interest rates is three percentage points.

On the Chinese fiscal stimulus memory hole

As evidence of China's growth slowdown mounts, Tyler Cowen asks why people no longer seem to be talking about that country's much-heralded fiscal stimulus of 2008-2009. I put the question to China expert Yi Wen, my colleague here in the research division of the St. Louis Fed. I thought it would be of some interest to share what he had to say. DA

There are several issues involved here regarding China’s economic performance and the effects of its stimulus packages.

1) As the following graph shows, 5 years after the financial crisis, U.S. industrial production remained 1.3 percent below its peak level; Industrial output in the EU remains at 12.2 percent below its level five years ago; Japan’s industrial production remains at 19.2 percent, below its level; China’s industrial output is 76.1 percent above the level five years previously. Recall that these regions were and are still china’s largest trading partners and China’s total exports have declined permanently by more than 40% since the crisis and still not recovered.

China’s industrial production therefore increased by over three quarters during a period when U.S. industrial production stagnated and EU and Japanese industrial production significantly declined. That is a conclusive success for China in this competitive struggle.

2) China’s stimulus package was designed to spend mainly on infrastructure buildup during a period when the costs of investment financing (borrowing) were the lowest. Since the operation of China’s first high-speed railroad merely six years ago, 28 Chinese provinces are now already covered by the world largest and longest high-speed rail network (more than ten thousand miles, greater than 50% of existing world capacity). If China had waited instead for 10 more years to do this, the costs would be many, many times higher.

3) Those being said, China today indeed faces the problem of excess industrial capacity, similar to US and European nations and Japan before WWI. China’s strategy to solve this excess capacity problem is to build a global infrastructure system (through so called “one belt, one road” program) that integrates the entire Eurasia continent and the Indian and Atlantic oceans transports, e.g., a full-fledged speed-train network stretching all the way south to Singapore and north to Russia and east to Europe is already under construction. This program is now backed by the newly established Asian Infrastructure Investment Bank (AIIB). This may look foolish to economists (remember China build the Great Wall for nothing J, not even shown up in GDP) but at least it will benefit global trade with significance no smaller than the Great Voyage. The age of maritime global trade (kick started by the Great Voyage) is perhaps going to be replaced or enhanced by cross continent land trade (a revision to the ancient Eurasian trade through the Silk Road).

To sum up, the Chinese appear to be more optimistic than the westerners, especially the well-trained economists, after 300 years of rejecting Capitalism (see my Working paper and forthcoming book: https://research.stlouisfed.org/wp/more/2015-006.  History will tell if they are right or not.